Question

Image transcription textTest: Exam 1

Question 8 of 19
This test: 95 point(s) possible
This question: 5 point(s) possible
estion list
K
Find the slope and y-intercept of the graph of the equation.
y = =x-1
Question 1
Slope = (Enter a fully reduced fraction.)
Question 2
y-intercept =
Question 3
Question 4
Question 5
Question 6
Question 7
Question 8... Show moreImage transcription texttion list
K
Determine the horizontal asymptote of the graph of the function.
f ( x ) = x - 4x2 + x - 3
estion 1
x2 - 12
estion 2
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
O A. The horizontal asymptote is y =
Jestion 3
(Type an integer or a fraction.)
O B. There is no horizontal asymptote.
uestion 4
Question 5
Question 6
Question 7
Question 8
Question 9
Time Remaining:... Show moreImage transcription textstion list
K
Find the domain of the function.
x - 7
f ( x ) = _
* +4
Question 2
The domain of f(x) = is.
Question 3
(Type your answer in interval notation.)
Question 4
Question 5
Question 6
Question 7
Question 8
O Question 9... Show moreImage transcription textest.
estion list
K
Describe verbally the transformations that can be used to obtain the graph of g from the graph of f.
g (x) = 3*+4; f(x) = 3x
Question 3
The graph of g is the graph of f shifted units
Question 4
Question 5
Question 6
Question 7
O Question 8
O Question 9
O Question 10... Show morePlease hel!

Answer 1

1. Slope = 1

2. y-intercept = -1

3. Horizontal asymptote is y = -4/1

4. Domain of f(x) = (-∞, ∞)

5. Transformations for g(x) = 3x + 4 from f(x) = 3x: Shifted 4 units upward.

In the given equation
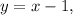`\( y = x - 1 \),` the slope-intercept form is
`\( y = mx + b \)`, where
`\( m \)` is the slope and
`\( b \)` is the y-intercept. Comparing with the given equation, we can see that the slope
`\( m \)` is 1, and the y-intercept \
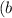`( b \)` is -1. Therefore, the final answers are: Slope = 1 and y-intercept = -1.

For the function
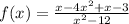`\( f(x) = (x - 4x^2 + x - 3)/(x^2 - 12) \)`, to find the horizontal asymptote, we need to compare the degrees of the numerator and denominator. As the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is the ratio of the leading coefficients, which is \(-4/1\). So, the horizontal asymptote is
`\( y = -4/1 \).`

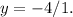
For the function
`\( f(x) = (x - 7)/(x + 4) \)`, the domain is all real numbers except where the denominator is zero. Therefore, the domain is
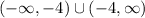`\( (-\infty, -4) \cup (-4, \infty) \)`, which can be expressed in interval notation as
`\( (-\infty, -4) \cup (-4, \infty) \).`

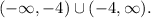
Finally, for
`\( g(x) = 3x + 4 \)`transformed from
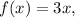`\( f(x) = 3x \),` the transformation involves shifting the graph 4 units upward. The addition of 4 to the original function results in the upward shift. Therefore, the answer is that the graph of
`\( g \)`is the graph of
`\( f \)` shifted 4 units upward.

Complete question:

Certainly! It seems that the text you provided is part of a set of questions related to mathematical functions and graphs. Here are the complete questions based on the information you provided:

Test: Exam 1

Question 8 of 19

This test: 95 point(s) possible

This question: 5 point(s) possible

Question List:

Find the slope and y-intercept of the graph of the equation.

`\[y = (x)/(x-1)\]`

Question 1

Slope = (Enter a fully reduced fraction.)

Question 2

y-intercept = ?

Question 3

...

---

Determine the horizontal asymptote of the graph of the function.

`\[f(x) = (x - 4x^2 + x - 3)/(x^2 - 12)\]`

Question 1

Horizontal asymptote = ?

Question 2

Select the correct choice below and, if necessary, fill in the answer box to complete your choice.*

O A. The horizontal asymptote is \(y = \_\_\_\_\) (Type an integer or a fraction.)

O B. There is no horizontal asymptote.

Question 3

...

---

Find the domain of the function.

`\[f(x) = (x - 7)/(x + 4)\]`

Question 1

The domain of \(f(x)\) is?

Question 2

(Type your answer in interval notation.)

Question 3

...

---

Describe verbally the transformations that can be used to obtain the graph of \(g\) from the graph of \(f\).

`\[g(x) = 3f(x) + 4; \quad f(x) = 3x\]`

Question 3

The graph of \(g\) is the graph of \(f\) shifted \_\_\_\_ units.

Question 4

...

---

I've included placeholders for the questions that were not provided in your initial message. If you have the complete text of those questions, feel free to share them, and I'll be happy to help further!