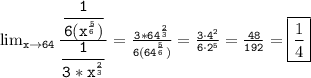Lim \frac{ \sqrt[6]{x} - 2}{ \sqrt[3]{x} - 4} x-->64 Please help!​

Question

Lim
`\frac{ \sqrt[6]{x} - 2}{ \sqrt[3]{x} - 4}`

x-->64

Please help!​

Answer 1

`\boxed{\tt (1)/(4)}`

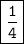
Explanation:

`\tt \lim_(x \to 64) \frac{\sqrt[6]{x}-2 }{\sqrt[3]{x}-4 }`

let's make the root in terms of Power.

`\tt \lim_(x \to 64) \frac{\sqrt[6]{x}-2 }{\sqrt[3]{x}-4 } = \lim_(x \to 64) \frac{x^{(1)/(6)}-2}{x^{(1)/(3)}-4}`

Using L' Hospital's rule, we need to take the derivative of the numerator and the derivative of the denominator separately.

• 
  `\tt (d)/(dx) \left[ x^{(1)/(6)}-2 \right] = (1)/(6)x^{(1)/(6)-1}-0 = (1)/(6)x^{(-5)/(6)}= \frac{1}{6(x^{(5)/(6)})}`

• 
  `\tt (d)/(dx) \left[ x^{(1)/(3)}-4 \right] = (1)/(3)x^{(-2)/(3)} = \frac{1}{3(x^{(2)/(3)})}`

So, the limit expression becomes:

`\tt \lim_(x \to 64) \frac{(d)/(dx) \left[ x^{(1)/(6)}-2 \right]}{(d)/(dx) \left[ x^{(1)/(3)}-4 \right]} = \lim_(x \to 64) \frac{\frac{1}{6(x^{(5)/(6)})}}{\frac{1}{3*x^{(2)/(3)}}}`

Now we can substitute x=64 into the limit expression, and we get:

`\tt \lim_(x \to 64) \frac{\frac{1}{6(x^{(5)/(6)})}}{\frac{1}{3*x^{(2)/(3)}}}=\frac{3*64^{(2)/(3)}}{6(64^{(5)/(6)})}= (3 \cdot 4^2)/(6 \cdot 2^5) = (48)/(192) = \boxed{(1)/(4)}`