Question

Determine the type of solutions the equation will have using the discriminant.

3x^2 + 5x + 8 = 0
A) One real root
B) Two real roots
C) Two complex roots

Answer 1

Answer is :

• Two complex roots.

Explanation:

3x²+ 5x + 8 = 0

On comparing this equation by ax² + bx + x = 0 W e obtained, a = 3, b = 5 and c = 8

Remember that,

The nature of the roots of the quadratic equation based on the coefficient is determined by the discriminant.

if b² - 4ac > 0, two Distinct real roots,

if b² - 4ac = 0, Two equal real roots,

if b² - 4ac < 0,No real roots or two complex roots

Discriminant = b² - 4ac

`\sf D = (5)^2 - 3 * 2 * 8`

`\sf D = 25 - 48`

`\sf D = - 23`

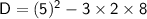
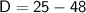
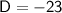
Since, b² - 4ac < 0

`\therefore` The given equation has Two complex roots