Question

20. Assume that all segments that appear to be tangent are. Find the value of x.

x = 20.3
x = 14.2
x = 21.1
x =8.9​

Answer 1

the answer is :

• 14.2

Explanation:

When we draw a radius at the point of the tangency , the angle formed between the tangent and radius will always be 90°

Therefore, In the given figure, it is a right angled triangle where,

KL = 7 + 11 = 18 (Hypotenuse)

JK = x (Base)

JL = 11 (Perpendicular)

As per pythagoras theorem,

`\sf (H)^2 = (P)^2 + (B)^2`

`\sf (18)^2 = (11)^2 + (x)^2`

`\sf 324 = 121 + x^2`

`\sf 324 - 121 = x^2`

`\sf 203 = x^2`

`\sf x = √(203)`

x = 14.2

`\therefore`The value of x is 14.2

Answer 2

x ≈ 14.2

Explanation:

assuming JK is a tangent then the angle between JK and the radius JL at the point of contact J is right.

then Δ JKL is a right triangle with hypotenuse KL

with KL = 7 + 11 = 18 ( internal part is a radius of the circle )

using Pythagoras' identity in the right triangle

JK² + JL² = KL² , that is

x² + 11² = 18²

x² + 121 = 324 ( subtract 121 from both sides )

x² = 203 ( take square root of both sides )

x =
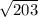`√(203)` ≈ 14.2 ( to the nearest tenth )