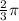Answer:
x = 0, π,2π
Explanation:
Given:
sin 2x+sin x=0
- we have Sin 2x= 2sinx cosx
2sinx cosx +sin x =0
Taking common sin x.
Sin x( 2cos x+1)=0
either
sinx = 0
or
2cosx + 1 = 0
If sinx = 0, then x = 0, π, or 2π.
If 2cosx + 1 = 0, then
cosx = -1/2.
x = cos (180-60)=cos 120 =-1/2
The cosine of 60 degrees is negative in quadrant 2.
In terms of π
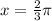
Therefore,
The value of x is 0, π,2π or