Question

Given f(x) and g(x) = kf(x), use the graph to determine the value of k.

Two lines labeled f of x and g of x. Line f of x passes through points negative 4, 0 and negative 2, 2. Line g of x passes through points negative 4, 0 and negative 2, negative 10.

−5
-1/5
1/5
5

Answer 1

k = -5

Explanation:

The slope of a line is a measure of its steepness. Mathematically, it is calculated as the change in y-values divided by the change in x-values ("rise over run").

From observation of the given graph, we can see that the slope of function f(x) is positive, and the slope of function g(x) is negative.

For function f(x), we can see that when the value of x increases by 1, the value of y always increases by 1. Therefore, the slope for f(x) is m = 1.

For function g(x), we can see that when the value of x increases by 1, the value of y always decreases by 5. Therefore, the slope for f(x) is m = -5.

Given f(x), and g(x) = kf(x), then the value of k is -5.

`\hrulefill`

Additional information

By using the found slopes, given points, and the slope-intercept formula, we can determine the equations for the functions:

`f(x) = x + 4`

`g(x) = -5x - 20=-5(x+4)`

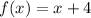
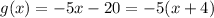
Therefore, we can see that g(x) is f(x) multiplied by -5. Thus confirming that k = -5.