Question

Thomas needs to buy a cardboard sheet that will allow him to make his 224 in^3 box.To help construct the box, he needs to cut out 2 inch squares from both the lengths and widths on all sides and then fold them up to make a box. Given that the length will need to be 6 inches longer than the width create an equation for the volume of the box, find the zeroes, the dimensions of the box, and graph the function.

Answer 1

Zeroes: x = -10, x = 12

Dimensions of the box: 8 in (W) x 14 in (L) x 2 in (H)

Explanation:

Let x be the width of the cardboard sheet.

Given the length is 6 inches longer than the width, then the length of the cardboard sheet is (x + 6).

To construct the box, Thomas needs to cut out 2 inch squares from the corners of the cardboard sheet. This means the height of the box is 2 inches, and the width and length of the box are 4 inches less than the width and length of the sheet.

Therefore, the dimensions of the box (in inches) are:

• Width = x - 4
• Length = (x + 6) - 4 = x + 2
• Height = 2

The box can be modelled as a rectangular prism.

The volume of a rectangular prism is the product of its width, length and height. Therefore, the function for the volume of the box is:

`\begin{aligned}\textsf{Volume}&=\sf width \cdot length \cdot height\\&=(x-4)(x+2)2\\&=2(x^2+2x-4x-8)\\&=2x^2-4x-16\end{aligned}`

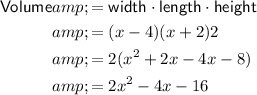
Given the volume of the box is 224 in³, we can say that:

`2x^2-4x-16=224`

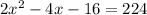
Solve the equation for x by factoring the quadratic and applying the zero-product property:

`\begin{aligned}2x^2-4x-16&=224\\2x^2-4x-16-224&=0\\2x^2-4x-240&=0\\2(x^2-2x-120)&=0\\x^2-2x-120&=0\\x^2+10x-12x-120&=0\\x(x+10)-12(x+10)&=0\\(x-12)(x+10)&=0\\\\x-12&=0\implies x=12\\x+10&=0 \implies x=-10\end{aligned}`

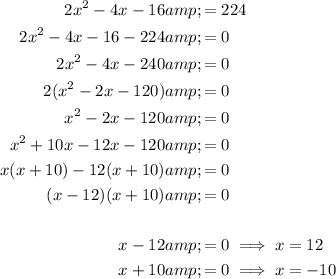
Therefore, the zeroes of the quadratic equation are x = 12 and x = -10.

As length is positive, the only valid x-value is x = 12.

To find the dimensions of the box, substitute x = 12 into the expressions for width and length:

`\begin{aligned}\textsf{Width}&=x-4\\&=12-4\\&=8\; \sf inches\end{aligned}`

`\begin{aligned}\textsf{Length}&=x+2\\&=12+2\\&=14\; \sf inches\end{aligned}`

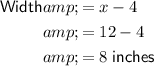
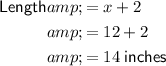
Therefore, the dimensions of the box are:

• Width = 8 inches
• Length = 14 inches
• Height = 2 inches

`\hrulefill`

Note: It is not clear from the question if the function that should be graphed is the general function for volume, or the function when the volume is fixed at 224 in³ (showing the zeroes as -10 and 12). Therefore, I have provided both.

The first graph shows the function for volume, where x is the variable. To find the values of x when y = 224, find the points of intersection with the line y = 224. This graph clearly shows that when y = 224, x = -10 and x = 12.

The second graph shows the function when the volume is fixed at 224 in³. The zeroes of this graph are the x-values of the fixed volume.