Question

A sculptor makes a miniature model before starting the final version. Her model is scaled so that of 1/4 of an inch corresponds to 6 feet on the final version. The base of her model is 5/12 of an inch. How big will the base of the final be?

Answer 1

10 feet

Explanation:

To find out the size of the base of the final version, we need to determine the scaling factor between the model and the final version.

Given that 1/4 of an inch on the model corresponds to 6 feet on the final version, we can set up the following proportion:

`(1/4 \ in)/( 6 \ ft) = ( 5/12 \ in )/( x )`

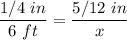
To solve for x, we cross-multiply:

`\Longrightarrow (1/4 \ in)(x)= (5/12 \ in)(6 \ ft)`

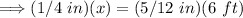
Now, let's simplify the equation:

`\Longrightarrow \Big((1)/(4) \ in\Big)(x )= \Big(\frac52 \ ft \cdot in\Big)`

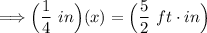
To eliminate the fraction, we can multiply both sides of the equation by 4:

`\Longrightarrow \Big((1)/(4) \ in\Big)(x)= \Big(\frac52 \ ft \cdot in\Big)\\\\\\\\\Longrightarrow x= \Big(\frac52 \ ft \cdot in\Big)\Big(4 \ in^(-1) \Big)\\\\\\\\\therefore \boxed{\boxed{x=10 \ ft}}`

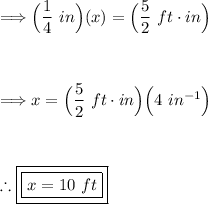
Therefore, the base of the final version will be 10 feet.