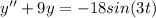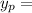Question

Find a particular solution to y ′′
+9y=−18sin(3t) y p
=

Answer 1

The particular solution to
`\(y'' + 9y = -18\sin(3t)\)` is
`\(y_p = \sin(3t) - \cos(3t)\)`.

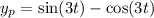To find the particular solution
`\(y_p\)` to the differential equation
`\(y'' + 9y = -18\sin(3t)\)`, let's first determine the form of the particular solution based on the form of the right-hand side function.

Given the form of the non-homogeneous term
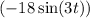`(\(-18\sin(3t)\))`, since the differential equation involves a sinusoidal function with a frequency of 3, the particular solution will also take the form of a sinusoidal function but with modified coefficients to fit the equation.

Let's assume a particular solution of the form
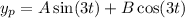`\(y_p = A\sin(3t) + B\cos(3t)\)`, where A and B are constants to be determined.

Now, let's find the first and second derivatives of \(y_p\) to substitute them into the differential equation and solve for \(A\) and \(B\).

`\[y_p = A\sin(3t) + B\cos(3t)\]`

`\[y_p' = 3A\cos(3t) - 3B\sin(3t)\]`

`\[y_p'' = -9A\sin(3t) - 9B\cos(3t)\]`

Substitute these derivatives into the differential equation
`\(y'' + 9y = -18\sin(3t)\)`:

`\[-9A\sin(3t) - 9B\cos(3t) + 9(A\sin(3t) + B\cos(3t)) = -18\sin(3t)\]`

Simplify the equation:

`\((-9A + 9B)\sin(3t) + (-9B - 9A)\cos(3t) = -18\sin(3t)\)`

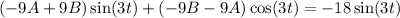
By comparing coefficients of sine and cosine terms separately:

For the sine term: -9A + 9B = -18

For the cosine term: -9B - 9A = 0

Solve these equations simultaneously:

From -9A - 9B = 0, we get A = -B. Substitute this into the first equation:

-9A + 9B = -18

-9A + 9(-A) = -18

-18A = -18

A = 1

Since A = -B, B = -1.

Therefore, the particular solution
`\(y_p\)` is:

`\[y_p = \sin(3t) - \cos(3t)\]`

Question:

Find a particular solution to
`y''+9y=-18sin(3t)`

`y_p =`