Question

2. Using method of undetermined coefficients (NOTE: if you use other method, you won't get credit for this problem) to find general solutions to \[ y^{\prime \prime}-2 y^{\prime}-3 y=3 e^{2 t} . \]

Answer 1

The general solution to the differential equation is:

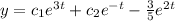`\(y = c_1e^(3t) + c_2e^(-t) - (3)/(5)e^(2t)\)`, where
`\(c_1\)` and
`\(c_2\)` are arbitrary constants.

To find the general solution to the differential equation
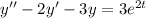`\(y'' - 2y' - 3y = 3e^(2t)\)` using the method of undetermined coefficients, we assume a particular solution in the form of
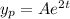`\(y_p = Ae^(2t)\)`, where
`\(A\)` is a constant to be determined.

We start by finding the derivatives of
`\(y_p\)`:

`\(y_p' = 2Ae^(2t)\)`

`\(y_p'' = 4Ae^(2t)\)`

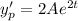
Substituting these derivatives into the original differential equation, we have:

`\(4Ae^(2t) - 2(2Ae^(2t)) - 3(Ae^(2t)) = 3e^(2t)\)`

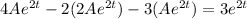
Simplifying the equation, we get:

`\(-2Ae^(2t) - 3Ae^(2t) = 3e^(2t)\)`

`\((-5A)e^(2t) = 3e^(2t)\)`

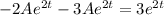
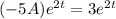
To satisfy this equation, we must have
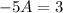`\(-5A = 3\)`, which gives
`\(A = -(3)/(5)\).`

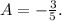
Therefore, the particular solution is
`\(y_p = -(3)/(5)e^(2t)\).`

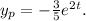
The general solution to the original differential equation is the sum of the complementary function and the particular solution:

`\(y = y_c + y_p\)`

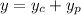
The complementary function is found by solving the homogeneous equation
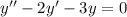`\(y'' - 2y' - 3y = 0\)`. Its characteristic equation is
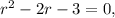`\(r^2 - 2r - 3 = 0\),`which factors as
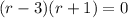`\((r - 3)(r + 1) = 0\)`. Thus, the complementary function is given by
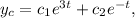`\(y_c = c_1e^(3t) + c_2e^(-t)\),` where
`\(c_1\)` and
`\(c_2\)` are arbitrary constants.

Therefore, the general solution to the differential equation is:

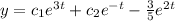`\(y = c_1e^(3t) + c_2e^(-t) - (3)/(5)e^(2t)\)`, where
`\(c_1\)` and
`\(c_2\)` are arbitrary constants.

Learn more about general solution here:

Using method of undetermined coefficients (NOTE: if you use other method, you won't get credit for this problem) to find general solutions to
`\[ y^(\prime \prime)-2 y^(\prime)-3 y=3 e^(2 t) . \]`