Question

Please help with the attached math problem

Answer 1

x=160 and y=90

Explanation:

To solve the system of equations using the inverse matrix method, we first need to represent the system in matrix form. Let's define the coefficient matrix A, the variable matrix X, and the constant matrix B as follows:

Given:

`\left\{\begin{array}{ccc}3x-5y=30\\7x-12y=40\end{array}\right`

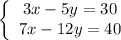
In matrix form:

`\left[\begin{array}{ccc}3&-5\\7&-12\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] =\left[\begin{array}{ccc}30\\40\end{array}\right]`

The system can be written as AX = B. To find the inverse of matrix A, we can use the formula:

`A^(-1) = (1)/(det(A)) \cdot adj(A)`

Where...

• "det(A)" represents the determinant of matrix A
• "adj(A)" represents the adjugate of matrix A.

Now, let's find the inverse of matrix A:

1. Calculate the determinant of A:

`det(A)=(3)(-12)-(-5)(7)=-36-(-35)\\\\\\\therefore det(A)=-1`

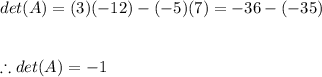
2. Calculate the adjugate of A:

`adj(A)= \left[\begin{array}{ccc}-12&5\\-7&3\end{array}\right]`

3. Calculate the inverse of A:

`A^(-1) = (1)/(det(A)) \cdot adj(A)\\\\\\\Longrightarrow A^(-1)=(1)/(-1)\left[\begin{array}{ccc}-12&5\\-7&3\end{array}\right]\\\\\\ A^(-1)=-1\cdot\left[\begin{array}{ccc}-12&5\\-7&3\end{array}\right]\\\\\\\therefore A^(-1)=\left[\begin{array}{ccc}12&-5\\7&-3\end{array}\right]`

Now that we have the inverse matrix, we can solve for X by multiplying both sides of the equation AX = B by A^(-1):

`A^(-1) \cdot AX = A^(-1) \cdot B\\\\\Longrightarrow \boxed{X = A^(-1) \cdot B}`

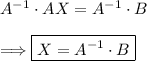
Substituting the values:

`\left[\begin{array}{ccc}x\\y\end{array}\right] =\left[\begin{array}{ccc}12&-5\\7&-3\end{array}\right]\left[\begin{array}{ccc}30\\40\end{array}\right]`

Performing the matrix multiplication:

`\Longrightarrow\left[\begin{array}{ccc}x\\y\end{array}\right] =\left[\begin{array}{ccc}(12)(30)-(5)(40)\\(7)(30) - (3)(40)\end{array}\right]\\\\\\\Longrightarrow\left[\begin{array}{ccc}x\\y\end{array}\right] =\left[\begin{array}{ccc}360 + (-200)\\210 + (-120)\end{array}\right]\\\\\\\therefore \boxed{\boxed{\left[\begin{array}{ccc}x\\y\end{array}\right] = \left[\begin{array}{ccc}160\\90\end{array}\right]}}`

Thus, x=160 and y=90.