Question

Find the values of p and q such that

4x^2+12x=4(x+p)^2-q

Answer 1

p=1.5 q=9

Explanation:

expand expression: 4x^+12x=4(x^2+2xp+p^2)-q

4x^2+12x=4x^2+8px+4p^2-q

4x^2+12x-4x^2-8px-4p^2+q=0

12x-8px-4p^2+q=0

q=-12x+8px+4p^2
q+12x-8px-4p^2=0

-8px-4p^2=-q-12x

Answer 2

`p=(3)/(2), \quad q=9`

Explanation:

Given equation:

`4x^2+12x=4(x+p)^2-q`

Expand the right side of the equation:

`\begin{aligned}4x^2+12x&=4(x+p)^2-q\\&=4(x+p)(x+p)-q\\&=4(x^2+2px+p^2)-q\\&=4x^2+8px+4p^2-q\end{aligned}`

Compare the corresponding terms on both sides:

`4x^2=4x^2`

`12x=8px`

`0=4p^2-q`

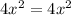
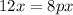
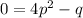
Solve the second equation for p:

`\begin{aligned}12x&=8px\\\\12&=8p\\\\p&=(12)/(8)\\\\p&=(12/ 4)/(8/ 4)\\\\p&=(3)/(2)\end{aligned}`

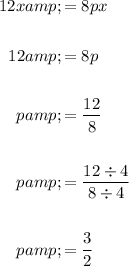
Substitute the found value of p into the third equation, and solve for q:

`\begin{aligned}0&=4p^2-q\\\\0&=4\left((3)/(2)\right)^2-q\\\\0&=4\left((3^2)/(2^2)\right)-q\\\\0&=4\left((9)/(4)\right)-q\\\\0&=9-q\\\\q&=9\end{aligned}`

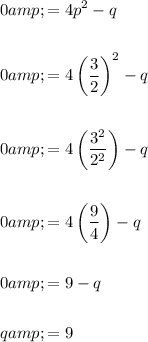
Therefore, the values of p and q that satisfy the equation are:

`p=(3)/(2), \quad q=9`