Answer:
Max (1,1)
Explanation:
The parabola is opening down, so this would be the highest point.
f(x) = -3
 + 6x - 2
+ 6x - 2
The x for the vertex is found
 b is 6 and a is -3
b is 6 and a is -3
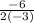 =
=
 = 1
= 1
The x value of the vertex is 1.
To find the y value, plug 1 in for x and solve for y
-3
 + 6x - 2
+ 6x - 2
-3(
 ) + 6(1) -2
) + 6(1) -2
-3 + 6 - 2
3 - 2
1
The y value of the vertex is 1.
The ordered pair for the vertex would be (1,1).
Helping in the name of Jesus.