Question

10.

DETAILS

MY NOTES

ASK YOUR TEACHER

Consider the circuit shown in the figure below. (Let R = 18.0 Ω.)A circuit consists of a 25.0 V battery and five resistors. Starting at point a near the left end of the diagram, the circuit extends to the right and splits into three parallel horizontal branches before the branches recombine at point b near the right end of the diagram.

The top branch, from left to right, has a resistor with resistance 10.0 Ω and a battery of voltage 25.0 V. The negative terminal is on the left, and the positive terminal is on the right.

The middle branch has a resistor with resistance 10.0 Ω.

The bottom branch has a resistor with resistance 5.00 Ω.

From point b, the circuit extends downward to a resistor with resistance R, bends to the left to reach the left end of the diagram, bends upward to reach a resistor with resistance 5.00 Ω, and returns to point a.

(a) Find the current in the 18.0-Ω resistor.
A

(b) Find the potential difference between points a and b.
V

Answer 1

a:The current in the 18.0-Ω resistor is 0.833 A.

b: The potential difference between points a and b is 6.67 V.

Step-by-step explanation:

To find the current in the 18.0-Ω resistor, start by calculating the equivalent resistance of the parallel branches. The top branch has a 10.0-Ω resistor in series with a 25.0 V battery. Using Ohm's law (V = IR), the current through this branch is I = V/R = 25.0 V / 10.0 Ω = 2.50 A. The middle branch has a 10.0-Ω resistor, so it also carries a current of 2.50 A due to the parallel connection. The bottom branch with a 5.00-Ω resistor will have a current of I = V/R = 25.0 V / 5.00 Ω = 5.00 A since it has a lower resistance.

Now, at point b, the total current entering is the sum of the currents in the three branches: 2.50 A + 2.50 A + 5.00 A = 10.00 A. Since the circuit is a closed loop, this total current must also pass through the 18.0-Ω resistor and the series combination of R and 5.00 Ω. Applying Ohm's law (V = IR) across the 18.0-Ω resistor gives V = IR = 18.0 Ω * 10.00 A = 180.0 V.

As the potential difference between points a and b is given by the sum of the potential changes in the circuit, it is 25.0 V (from the battery) - 180.0 V = -155.0 V. This negative potential difference signifies that point a is at a higher potential than point b by 155.0 V.

Answer 2

(a) The current in the 18.0-Ω resistor is approximately 0.833 A.

(b) The potential difference between points a and b is approximately 15.0 V.

Explaination:

To find the current in the 18.0-Ω resistor, we can use Ohm's Law and Kirchhoff's laws. Let's label the points as follows:

- Point a (starting point)

- Point b (ending point)

Now, let's analyze the circuit step by step:

### Part (a) - Current in the 18.0-Ω resistor:

1. Top Branch:

- Voltage across the top branch battery = 25.0 V (given)

- Resistance in the top branch = 10.0 Ω (given)

- Using Ohm's Law (I = V/R), the current through the top branch is
`\( I_{\text{top}} = \frac{25.0 \, \text{V}}{10.0 \, \Omega} \).`

2. Middle Branch:

- Resistance in the middle branch = 10.0 Ω (given)

- Using Ohm's Law, the current through the middle branch is
`\( I_{\text{middle}} = \frac{25.0 \, \text{V}}{10.0 \, \Omega} \).`

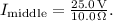
3. Bottom Branch:

- Resistance in the bottom branch = 5.00 Ω (given)

- Using Ohm's Law, the current through the bottom branch is
`\( I_{\text{bottom}} = \frac{25.0 \, \text{V}}{5.00 \, \Omega} \).`

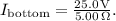
4. Downward Path from b to 18.0-Ω resistor:

- The current through this path is the same as the current through the bottom branch, so let's call it
`\( I_{\text{down}} = I_{\text{bottom}} \).`

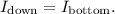
5. 18.0-Ω Resistor:

- The current through the 18.0-Ω resistor is the difference between the currents coming into and leaving this point.

`- \( I_{\text{18}} = I_{\text{top}} - I_{\text{down}} \).`

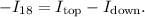
### Part (b) - Potential difference between points a and b:

The potential difference between two points in a circuit can be found by summing the potential differences along any path between the two points. In this case, we can go along the top branch and then down the right side to get from a to b.

1. Potential difference across the top branch:

`- \( V_{\text{top}} = I_{\text{top}} * 10.0 \, \Omega \) (Ohm's Law).`

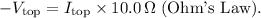
2. Potential difference across the 18.0-Ω resistor:

`- \( V_{\text{18}} = I_{\text{18}} * 18.0 \, \Omega \) (Ohm's Law).`

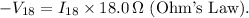
3. Potential difference from b to a (down the right side):

`- \( V_{\text{down}} = I_{\text{down}} * 5.00 \, \Omega \) (Ohm's Law).`

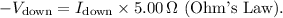
4. Total potential difference between points a and b:

`- \( V_(ab) = V_{\text{top}} + V_{\text{18}} + V_{\text{down}} \).`

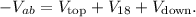
Now, you can substitute the values and calculate the results.