Question

Sandhill Corp. Will pay dividends of $5.00,$6.25,$4.75, and $3.00 in the next four years. Thereafter, management expects the dividend growth rate to be constant at 6 percent. If the required rate of return is 21.00 percent, what is the current value of the stock? (Round all intermediate calculations and final answer to 2 decimal places, es. 15.20.) Current value

Answer 1

To calculate the current value of the stock, we need to calculate the present value of the future dividends and the present value of the perpetuity. The current value of the stock is $27.44.

Step-by-step explanation:

To calculate the current value of the stock, we need to calculate the present value of the future dividends and the present value of the perpetuity. First, let's calculate the present value of the future dividends using the formula:

`PV = D1 / (1 + r) + D2 / (1 + r)^2 + D3 / (1 + r)^3 + D4 / (1 + r)^4`

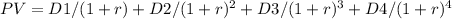
where D1, D2, D3, and D4 are the dividends for each year, and r is the required rate of return. Plugging in the given values:

`PV = $5.00 / (1 + 0.21) + $6.25 / (1 + 0.21)^2 + $4.75 / (1 + 0.21)^3 + $3.00 / (1 + 0.21)^4`

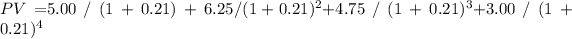
Solving this equation, we find that the present value of the future dividends is $13.15.

Next, let's calculate the present value of the perpetuity using the formula:

PV = D / r

where D is the dividend and r is the required rate of return. Plugging in the given values:

PV = $3.00 / 0.21

Solving this equation, we find that the present value of the perpetuity is $14.29.

Finally, let's add the present value of the future dividends and the present value of the perpetuity to get the current value of the stock:

Current value = $13.15 + $14.29 = $27.44

Therefore, the current value of the stock is $27.44.