1. The net work done is approximately
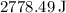 .
.
2. The final speed of the trunk after being pulled for 12.7 m is approximately
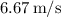 .
.
To find the net work done and the final speed of the trunk, let's break down the problem:
1. Net Work Done:
Net work is the work done by the applied force minus the work done against friction.
Work done by the applied force:
![\[ W_{\text{applied}} = F_{\text{applied}} * d * \cos(\theta) \]](https://img.qammunity.org/2024/formulas/physics/high-school/6ou41uwt8wxhmfmz3h4su41aeoy2e3z2ss.png)
Where:
-
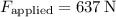
-
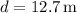
-
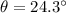
Work done against friction:
![\[ W_{\text{friction}} = \mu_k * N * d \]](https://img.qammunity.org/2024/formulas/physics/high-school/z694ylxkujfxsn9rhayzp8emxmm8tfbamc.png)
Where:
-
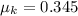 (coefficient of kinetic friction)
(coefficient of kinetic friction)
- N is the normal force (equal to the weight of the trunk, N = mg )
-
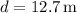
Net work done:
![\[ \text{Net Work} = W_{\text{applied}} - W_{\text{friction}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/e743em5pcl7zx31c0h6t8vceiles361kmp.png)
2. Final Speed of the Trunk:
The net work done is equal to the change in kinetic energy of the trunk. Using the work-energy principle:
![\[ \text{Net Work} = \Delta KE = (1)/(2)mv_f^2 - (1)/(2)mv_i^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/dijaz74l3xuh2tclbr61kvm8g1pi0p1du5.png)
Where:
-
 (mass of the trunk)
(mass of the trunk)
-
 (initial speed, the trunk is initially at rest)
(initial speed, the trunk is initially at rest)
-
 is the final speed of the trunk
is the final speed of the trunk
Let's calculate these:
1. Net Work Done:
![\[ W_{\text{applied}} = 637 * 12.7 * \cos(24.3^\circ) \]](https://img.qammunity.org/2024/formulas/physics/high-school/vd99a8jdx5wk1ofx1z347lb1tz9xg4d8rm.png)
![\[ W_{\text{applied}} \approx 8106.94 \, \text{J} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ca5kp7mdv78q9jcn8qcwa9w2ml2mo57p3r.png)
Normal force
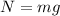
![\[ N = 125 * 9.81 \]](https://img.qammunity.org/2024/formulas/physics/high-school/ndlfc5y9tfu4iqq0v4s6bxkggxqan3apnc.png)
![\[ N \approx 1226.25 \, \text{N} \]](https://img.qammunity.org/2024/formulas/physics/high-school/sorwbdp5kfgm0k0lkpyy2a7wy17vk01vcm.png)
![\[ W_{\text{friction}} = 0.345 * 1226.25 * 12.7 \]](https://img.qammunity.org/2024/formulas/physics/high-school/q8yruvcpf1i6u8p05wsaemwwl2ukoifhhv.png)
![\[ W_{\text{friction}} \approx 5328.45 \, \text{J} \]](https://img.qammunity.org/2024/formulas/physics/high-school/g3uvif02i7v4g19k0jtnn9odtypjuy49m9.png)
Net Work:
![\[ \text{Net Work} = 8106.94 - 5328.45 \]](https://img.qammunity.org/2024/formulas/physics/high-school/2je68t5or6npk97etqbfoqyndyweh1kmef.png)
![\[ \text{Net Work} \approx 2778.49 \, \text{J} \]](https://img.qammunity.org/2024/formulas/physics/high-school/dkwcwg2zkqakhmfsyw4vhlzeeokelugdsc.png)
2. Final Speed of the Trunk:
Using the work-energy principle:
![\[ \text{Net Work} = (1)/(2)mv_f^2 - (1)/(2)mv_i^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/co87etz2gtf901r6yjdm2bm042cwgc1dzq.png)
![\[ 2778.49 = (1)/(2) * 125 * v_f^2 - 0 \]](https://img.qammunity.org/2024/formulas/physics/high-school/6bnpa42jiooqurmdfe9rg0p3q20kigmeo9.png)
![\[ v_f^2 = (2 * 2778.49)/(125) \]](https://img.qammunity.org/2024/formulas/physics/high-school/qb03tvimjhcht15dcj99wzvydhnlgke3u3.png)
![\[ v_f^2 \approx 44.46 \]](https://img.qammunity.org/2024/formulas/physics/high-school/bjlaf5h3hzo2qx97sg7t7jznvu22qq51at.png)
![\[ v_f \approx √(44.46) \]](https://img.qammunity.org/2024/formulas/physics/high-school/xtljpfg6s1d52tkns2d5twmbdkv511lqfw.png)
![\[ v_f \approx 6.67 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/high-school/jk3qfv1fsyxee0ykc0c9e8uuss1i5ndd60.png)