Answer:
Approximately
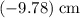 (
(
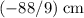 .)
.)
Step-by-step explanation:
At a distance of
 , the electric field
, the electric field
 resulting from point charge
resulting from point charge
 would be
would be
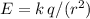 , where
, where
 is the Coulomb constant.
is the Coulomb constant.
When two point charges are placed near each other, the resultant electric field would be the vector sum of the field from each charge.
Let
 denote the coordinate where the resultant fields is
denote the coordinate where the resultant fields is
 . At this position, the distance from
. At this position, the distance from
 would be
would be
 , while the distance from
, while the distance from
 would be
would be
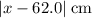 .
.
Assume that either
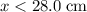 or
or
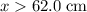 , such that both
, such that both
 and
and
 are on the same side of this position. The two electric fields would originate from the same side of this position. For the resultant electric field to be zero, set the sum of the two electric fields to be zero:
are on the same side of this position. The two electric fields would originate from the same side of this position. For the resultant electric field to be zero, set the sum of the two electric fields to be zero:
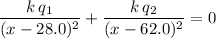 .
.
Since
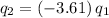 :
:
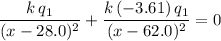 .
.
Simplify and solve for
 :
:
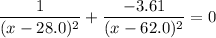 .
.
The two roots are
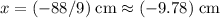 and
and
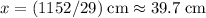 . However, only
. However, only
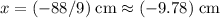 is valid under the assumption that either
is valid under the assumption that either
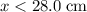 or
or
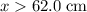 . A positive point charge at
. A positive point charge at
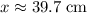 (between
(between
 and
and
 ) would be attracted towards
) would be attracted towards
 while simultaneously repelled from
while simultaneously repelled from
 , such that the resultant force would be non-zero.
, such that the resultant force would be non-zero.
Assume that
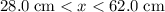 , such that this position is between
, such that this position is between
 and
and
 . The electric fields would originate from two different sides of this position. In the equation, the sign of one of the two fields would need to be flipped since the two fields are from two opposite directions:
. The electric fields would originate from two different sides of this position. In the equation, the sign of one of the two fields would need to be flipped since the two fields are from two opposite directions:
 .
.
Simplify and solve for
 :
:
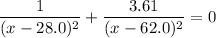 .
.
Since both fractions are greater than zero, no real solution exists in this scenario. In other words, the electric field is non-zero when
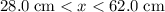 .
.
Therefore, the only position where the electric field is zero would be
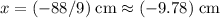 .
.