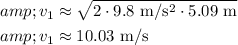Question

Two blocks of masses m1 = 1.86 kg and m2 =

4.34 kg are each released from rest at a height of h = 5.09 m on a
frictionless track, as shown in the figure, and undergo an elastic
head-on collision.
D

Answer 1

For two blocks undergoing an elastic head-on collision, their final velocities can be calculated using the conservation of momentum and kinetic energy.

Step-by-step explanation:

A head-on elastic collision occurs when two objects collide and separate after the collision, conserving both momentum and kinetic energy. In this case, two blocks of masses m1 = 1.86 kg and m2 = 4.34 kg are released from rest at a height of h = 5.09 m on a frictionless track. When they collide elastically, their final velocities can be determined using the conservation of momentum and kinetic energy.

Using the principles of conservation of momentum and kinetic energy, we have:

m1 * v1i + m2 * v2i = m1 * v1f + m2 * v2f (conservation of momentum)

0.5 * m1 * v1i2 + 0.5 * m2 * v2i2 = 0.5 * m1 * v1f^2 + 0.5 * m2 * v2f2 (conservation of kinetic energy)

By substituting the known values, the final velocities of the masses after the collision can be calculated.

Answer 2

The velocity of the
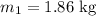`\(m_1 = 1.86 \ \text{kg}\)` block just before the collision is approximately
`\(10.03 \ \text{m/s}\)`.

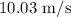To determine the velocity of the
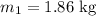`\(m_1 = 1.86 \ \text{kg}\)` block just before the collision, we can use the principle of conservation of mechanical energy. The initial potential energy
`\(mgh\)` is converted into kinetic energy just before the collision.

The potential energy at height (h) is given by (mgh), where:

m is the mass of the block,

g is the acceleration due to gravity, and

h is the height.

The kinetic energy just before the collision is given by
`\((1)/(2)mv^2\)`, where:

(m) is the mass of the block, and

(v) is its velocity.

According to the conservation of mechanical energy, the potential energy lost by
`\(m_1\)` is equal to the kinetic energy gained by
`\(m_1\)`.

Therefore:

`\[ m_1gh = (1)/(2)m_1v_1^2 \]`

Let's solve for
`\(v_1\)`:

`\[ v_1 = √(2gh) \]`

Substitute the given values:

`\begin{aligned}& v_1 \approx \sqrt{2 \cdot 9.8 \mathrm{~m} / \mathrm{s}^2 \cdot 5.09 \mathrm{~m}} \\& v_1 \approx 10.03 \mathrm{~m} / \mathrm{s}\end{aligned}`