Question

Determine the equations of the bisectors of the angles between the lines 3x - 2y + 1 = 0 and 18x+y-5=0 . Identify the bisector of the acute angle.

Please help!
​

Answer 1

`\textsf{Equations of bisectors:}\quad \begin{cases}3x+11y-10=0\\33x-9y=0\end{cases}`

`\textsf{Bisector of acute angle:} \quad 33x - 9y = 0`

Explanation:

To determine the equations of the angle bisectors of two lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0, we can use the formula:

`\boxed{\frac{a_1x+b_1y+c_1}{\sqrt{{a_1}^2+{b_1}^2}}=\pm\frac{a_2x+b_2y+c_2}{\sqrt{{a_2}^2+{b_2}^2}}}`

Let line 3x - 2y + 1 = 0 be defined by the equation a₁x + b₁y + c₁ = 0.

Let line 18x + y - 5 = 0 be defined by the equation a₂x + b₂y + c₂ = 0.

Therefore:

• a₁ = 3
• b₁ = -2
• c₁ = 1
• a₂ = 18
• b₂ = 1
• c₂ = -5

Substitute the values of a₁, b₁, c₁, a₂, b₂, and c₂ into both formulas.

Equation of bisector 1

`\begin{aligned}\frac{3x-2y+1}{\sqrt{{3}^2+{(-2)}^2}}&=\frac{18x+y-5}{\sqrt{{18}^2+{1}^2}}}\\\\(3x-2y+1)/(√(13))&=(18x+y-5)/(5√(13))\\\\3x-2y+1&=(18x+y-5)/(5)\\\\5(3x-2y+1)&=18x+y-5\\\\15x-10y+5&=18x+y-5\\\\3x+11y-10&=0\end{aligned}`

Equation of bisector 2

`\begin{aligned}\frac{3x-2y+1}{\sqrt{{3}^2+{(-2)}^2}}&=-\frac{18x+y-5}{\sqrt{{18}^2+{1}^2}}}\\\\(3x-2y+1)/(√(13))&=-(18x+y-5)/(5√(13))\\\\3x-2y+1&=-(18x+y-5)/(5)\\\\5(3x-2y+1)&=-18x-y+5\\\\15x-10y+5&=-18x-y+5\\\\33x-9y&=0\end{aligned}`

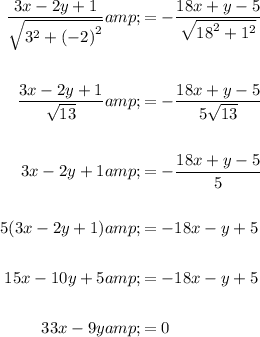
Therefore, the equations of bisectors of the angles between the given lines are:

`\boxed{\boxed{\begin{aligned}3x+11y-10&=0\\33x-9y&=0\end{aligned}}}`

`\hrulefill`

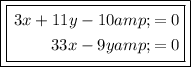
To identify the bisector of the acute angle, calculate the angle between any one of the bisectors and one of the lines.

The formula for the angle between two lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 is:

`\tan \theta=\left|(a_2b_1-a_1b_2)/(a_1a_2+b_1b_2) \right|`

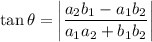
Let's find the angle θ between the bisector 3x + 11y - 10 = 0, and the line 3x - 2y + 1 = 0.

Therefore:

• a₁ = 3
• b₁ = 11
• a₂ = 3
• b₂ = -2

Substitute the values of a₁, b₁, a₂ and b₂ into the formula for the angle between two lines:

`\tan \theta=\left|(3 \cdot 11-3 \cdot (-2))/(3 \cdot 3+11\cdot (-2)) \right|`

`\tan \theta=\left|(33+6)/(9-22) \right|`

`\tan \theta=\left|(39)/(-13) \right|`

`\tan \theta=\left|-3\right|`

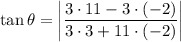
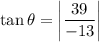
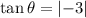
As tan θ > 1, the angle θ between the bisector and the line must be more than 45°. This means that the angle between the two given lines is more than 90°. So 3x + 11y - 10 = 0 is the bisector of the obtuse angle between the given lines. Therefore, the other angle bisector bisects the acute angle.

Therefore, the bisector of the acute angle is:

`\boxed{\boxed{33x - 9y = 0 }}`

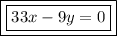
Note: The attached diagram shows the given lines as black lines, the bisector of the acute angle as the red dashed line, and the bisector of the obtuse angle as the green dashed line.