Question

2.0-cm-diameter copper ring has 8.0×10 9

excess Part A electrons. A proton is released from rest on the axis of the ring, 5.0 cm from its center. What is the proton's speed as it passes through the center of the ring? Express your answer with the appropriate units.

Answer 1

The speed of the proton as it passes through the center of the ring is approximately
`\( 8.65 * 10^6 \, \text{m/s} \)`.

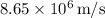To find the speed of the proton as it passes through the center of the ring due to the electrostatic force exerted by the excess electrons on the ring, we'll consider the electric potential energy converted to kinetic energy.

The potential energy U of the proton at a distance r from a charged ring is:

`\[ U = (k_e \cdot Q \cdot q)/(r) \]`

Where:

-
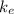`\( k_e \)` is Coulomb's constant
`(\( 8.99 * 10^9 \, \text{N m}^2/\text{C}^2 \))`

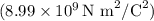
- Q is the total charge on the ring
`(\( Q = 8.0 * 10^9 \, \text{excess electrons} * e \), where \( e \) is the charge of an electron)`

- q is the charge of the proton
`(\( e = 1.6 * 10^(-19) \, \text{C} \))`

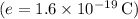
- r is the distance between the proton and the center of the ring
`(\( r = 5.0 \, \text{cm} = 0.05 \, \text{m} \))`

At the center of the ring, all the potential energy will be converted into kinetic energy.

`\[ U = (1)/(2) m v^2 \]`

Where:

- m is the mass of the proton
`(\( m = 1.67 * 10^(-27) \, \text{kg} \))`

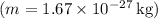
- v is the velocity of the proton

Equating these expressions, we can solve for v:

`\[ (k_e \cdot Q \cdot q)/(r) = (1)/(2) m v^2 \]`

`\[ v = \sqrt{(2 \cdot k_e \cdot Q \cdot q)/(m \cdot r)} \]`

Let's compute the value of v using these values.

The equation for the velocity of the proton as it passes through the center of the ring is:

`\[ v = \sqrt{(2 \cdot k_e \cdot Q \cdot q)/(m \cdot r)} \]`

Let's plug in the given values:

- Coulomb's constant
`\( k_e = 8.99 * 10^9 \, \text{N m}^2/\text{C}^2 \)`

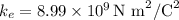
- Total charge on the ring
`\( Q = 8.0 * 10^9 \, \text{excess electrons} * e \)`

- Charge of the proton
`\( q = 1.6 * 10^(-19) \, \text{C} \)`

- Mass of the proton
`\( m = 1.67 * 10^(-27) \, \text{kg} \)`

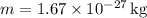
- Distance from the center of the ring
`\( r = 5.0 \, \text{cm} = 0.05 \, \text{m} \)`

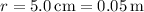
Let's calculate the value of v.

`\[ v = \sqrt{(2 \cdot k_e \cdot Q \cdot q)/(m \cdot r)} \]`

Given:

- Coulomb's constant
`\( k_e = 8.99 * 10^9 \, \text{N m}^2/\text{C}^2 \)`

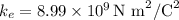
- Total charge on the ring
`\( Q = 8.0 * 10^9 \, \text{excess electrons} * e \)`

- Charge of the proton
`\( q = 1.6 * 10^(-19) \, \text{C} \)`

- Mass of the proton
`\( m = 1.67 * 10^(-27) \, \text{kg} \)`

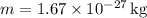
- Distance from the center of the ring
`\( r = 5.0 \, \text{cm} = 0.05 \, \text{m} \)`

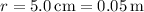
`\[ v = \sqrt{\frac{2 \cdot (8.99 * 10^9 \, \text{N m}^2/\text{C}^2) \cdot (8.0 * 10^9 \, \text{excess electrons} * 1.6 * 10^(-19) \, \text{C}) \cdot (1.6 * 10^(-19) \, \text{C})}{(1.67 * 10^(-27) \, \text{kg}) \cdot (0.05 \, \text{m})}} \]`

Let's calculate the value of v.

The calculation for the speed v of the proton as it passes through the center of the ring is:

`\[ v = \sqrt{\frac{2 \cdot (8.99 * 10^9 \, \text{N m}^2/\text{C}^2) \cdot (8.0 * 10^9 \, \text{excess electrons} * 1.6 * 10^(-19) \, \text{C}) \cdot (1.6 * 10^(-19) \, \text{C})}{(1.67 * 10^(-27) \, \text{kg}) \cdot (0.05 \, \text{m})}} \]`

Let's compute the value of v.

The speed v of the proton as it passes through the center of the ring is calculated using:

`\[ v = \sqrt{\frac{2 \cdot (8.99 * 10^9 \, \text{N m}^2/\text{C}^2) \cdot (8.0 * 10^9 \, \text{excess electrons} * 1.6 * 10^(-19) \, \text{C}) \cdot (1.6 * 10^(-19) \, \text{C})}{(1.67 * 10^(-27) \, \text{kg}) \cdot (0.05 \, \text{m})}} \]`

Calculating this yields:

`\[ v \approx 8.65 * 10^6 \, \text{m/s} \]`

Answer 2

The speed of the proton as it passes through the center of the ring is approximately 9.41 × 10⁵ m/s.

How to calculate the proton's speed?

Use the formula for the electric field due to a uniformly charged ring:

E = k × Q / (r²)

where:

k = Coulomb's constant (8.99 × 10⁹ N⋅m²/C²)

Q = total charge of the ring

r = distance from the center of the ring to the point where the electric field is measured

In this case:

Q = (8.0 × 10⁹ electrons) × (-e)

= -8.0 × 10⁹ × (1.602 × 10⁻¹⁹ C)

= -1.282 × 10⁻⁹ C

r = 5.0 cm

= 0.05 m

Therefore:

E = (8.99 × 10⁹ N⋅m²/C²) × (-1.282 × 10⁻⁹ C) / (0.05 m)²

E = 4.83 × 10⁴ N/C

The potential energy of the proton is given by:

U = q × E

where:

q = charge of the proton (1.602 × 10⁻¹⁹ C)

Therefore:

U = (1.602 × 10⁻¹⁹ C) × (4.83 × 10⁴ N/C)

U = 7.75 × 10⁻¹⁵ J

All the potential energy at the initial position is converted to kinetic energy at the center of the ring:

K = U

K = 7.75 × 10⁻¹⁵ J

The kinetic energy of the proton is given by:

K = 1/2 × m × v²

where:

m = mass of the proton (1.67 × 10⁻²⁷ kg)

v = speed of the proton

Therefore:

v = √(2 × K / m)

v = √(2 × (7.75 × 10⁻¹⁵ J) / (1.67 × 10⁻²⁷ kg))

v ≈ 9.41 × 10⁵ m/s

Therefore, the speed of the proton as it passes through the center of the ring is approximately 9.41 × 10⁵ m/s.