Question

A 6.3-kg bowling ball and a 7.1−kg bowling ball Part A rest on a rack 0.85 m apart. What is the force of gravity exerted on each of the balls by the other ball? Express your answer using two significant figures. Part B At what separation is the force of gravity between the balls equal to 1.9×10 −9

N ? Express your answer using two significant figures.

Answer 1

1. The force of gravity exerted on the 7.1 kg bowling ball by the 6.3 kg bowling ball is also approximately
`\(2.578 * 10^(-7) \, \text{N}\)`.

2. At a separation distance of approximately 1.496 meters, the force of gravity between the balls will be equal to
`\(2.0 * 10^(-9) \, \text{N}\)`.

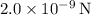To find the force of gravity between two objects, you can use Newton's law of universal gravitation, which is given by the formula:

`\[F = \frac{{G \cdot (m_1 \cdot m_2)}}{{r^2}}\]`

Where:

• F is the force of gravity between the two objects.
• G is the gravitational constant
  `(\(6.67430 * 10^(-11) \, \text{N}\cdot\text{m}^2/\text{kg}^2\))`.
• 
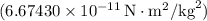  `\(m_1\)` and
  `\(m_2\)` are the masses of the two objects.
• r is the separation distance between the centers of the two objects.

a) To find the force of gravity exerted on each of the balls by the other ball, we will calculate the force for each pair of balls separately.

For the 6.3 kg bowling ball:

`\[F_1 = \frac{{G \cdot (m_1 \cdot m_2)}}{{r^2}}\]`

Substituting the values:

`\[F_1 = \frac{{6.67430 * 10^(-11) \, \text{N}\cdot\text{m}^2/\text{kg}^2 \cdot (6.3 \, \text{kg} \cdot 7.1 \, \text{kg})}}{{(0.85 \, \text{m})^2}}\]`

Now, calculate
`\(F_1\)`:

`\[F_1 \approx 2.578 * 10^(-7) \, \text{N}\]`

So, the force of gravity exerted on the 6.3 kg bowling ball by the 7.1 kg bowling ball is approximately
`\(2.578 * 10^(-7) \, \text{N}\)`.

For the 7.1 kg bowling ball:

`\[F_2 = \frac{{G \cdot (m_1 \cdot m_2)}}{{r^2}}\]`

Substituting the values:

`\[F_2 = \frac{{6.67430 * 10^(-11) \, \text{N}\cdot\text{m}^2/\text{kg}^2 \cdot (7.1 \, \text{kg} \cdot 6.3 \, \text{kg})}}{{(0.85 \, \text{m})^2}}\]`

Now, calculate
`\(F_2\)`:

`\[F_2 \approx 2.578 * 10^(-7) \, \text{N}\]`

So, the answer is approximately
`\(2.578 * 10^(-7) \, \text{N}\)`.

b) Now, let's find the separation distance at which the force of gravity between the balls is equal to
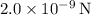`\(2.0 * 10^(-9) \, \text{N}\)`. We'll use the formula for F and solve for r:

`\[2.0 * 10^(-9) \, \text{N} = \frac{{6.67430 * 10^(-11) \, \text{N}\cdot\text{m}^2/\text{kg}^2 \cdot (6.3 \, \text{kg} \cdot 7.1 \, \text{kg})}}{{r^2}}\]`

Now, solve for r:

`\[r^2 = \frac{{6.67430 * 10^(-11) \, \text{N}\cdot\text{m}^2/\text{kg}^2 \cdot (6.3 \, \text{kg} \cdot 7.1 \, \text{kg})}}{{2.0 * 10^(-9) \, \text{N}}}\]`

`\[r^2 \approx \frac{{4.470609 * 10^(-9) \, \text{N}\cdot\text{m}^2/\text{kg}^2}}{{2.0 * 10^(-9) \, \text{N}}}\]`

`\[r^2 \approx 2.2353045 \, \text{m}^2\]`

Now, take the square root of both sides to find r:

`\[r \approx \sqrt{2.2353045 \, \text{m}^2} \approx 1.496 \, \text{m}\]`

So, The answer is approximately 1.496 meters.

The complete question is here:

A 6.3kg bowling ball and a 7.1 kg bowling ball rest on ar ack 0.85 m apart.

a) What is the force of gravity exerted on each of the balls by the other ball.

b) At what separation is the force of gravity between the balls equal to
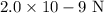`$2.0 * 10-9 \mathrm{~N}$`. Give complete answer step wise with proper calculations

Answer 2

A. The force of gravity exerted on each ball by the other is
`4.13*10^(-9)\ N`

B. The separation distance in which the gravity between them is
`1.9*10^(-9)\ N`, is 1.25 m

How to calculate the force of gravity and distance?

A. The force of gravity exerted on each ball by the other can be obtained as follow:

• Mass of first ball (M₁) = 6.3 Kg
• Mass of second object (M₂) = 7.1 Kg
• Distance apart (r) = 0.85 m
• Gravitational constant (G) =
  `6.67*10^(-11)\ Nm^2/Kg^2`
• Force of gravity (F) =?

`F = G(M_1M_2)/(r^2) \\\\F = 6.67*10^(-11)\ * (6.3\ * 7.1)/(0.85^2)\\\\F = 4.13*10^(-9)\ N\\\\`

B. The separation distance in which the gravity between them is
`1.9*10^(-9)\ N` can be calculated as follow:

• Mass of first ball (M₁) = 6.3 Kg
• Mass of second object (M₂) = 7.1 Kg
• Gravitational constant (G) =
  `6.67*10^(-11)\ Nm^2/Kg^2`
• Force of gravity (F) =
  `1.9*10^(-9)\ N`
• Distance apart (r) = ?

`r = \sqrt{(GM_1M_2)/(F)}\\\\r = \sqrt{(6.67*10^(-11)\ *\ 6.3\ *\ 7.1)/(1.9*10^(-9))}\\\\r = 1.25\ m`