Question

In order to take a nice warm bath, you mix 50 liters of hot water at 55 ∘

C with 25 liters of cold water at 10 ∘
C. How much new entropy have you created by mixing the water?

Answer 1

Mixing hot and cold water increases the overall entropy of the system.

Step-by-step explanation:

Entropy is a measure of the disorder or randomness in a system. The increase in entropy is due to the mixing of two bodies of water, which results in an overall increase in entropy. When you mix 50 liters of hot water at 55°C with 25 liters of cold water at 10°C, the hot water loses some of its entropy, while the cold water gains even more entropy. This leads to an increase in the overall entropy of the system.

Answer 2

You have created approximately 137.4 J/K of new entropy by mixing the hot and cold water.

How to find new entropy?

Calculating the Change in Entropy

To calculate the change in entropy (ΔS) when mixing the hot and cold water, we can use the following formula:

`\Delta S = S_(final) - (S_(hot) + S_(cold))`

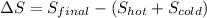
where:

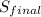`S_{final` = total entropy of the mixture

`S_{hot` = entropy of the hot water

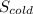`S_{cold` = entropy of the cold water

Use the formula for the entropy of an ideal gas:

`S = k * ln(V) + C_v * ln(T)`

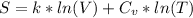
where:

k = Boltzmann's constant (1.38 × 10^-23 J/K)

V = volume of the water

`C_v` = heat capacity at constant volume (4.184 J/g°C for water)

T = temperature in Kelvin (K)

For the hot water:

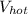`V_{hot` = 50 liters

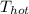`T_{hot` = 55°C + 273.15 = 328.15 K

`S_(hot) = k * ln(V_(hot)) + C_v * ln(T_(hot))`

`S_{hot` = 1.38 × 10⁻²³ J/K × ln(50 liters) + 4.184 J/g°C × ln(328.15 K)

`S_{hot` = 658.7 J/K

For the cold water:

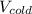`V_{cold`= 25 liters

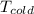`T_{cold` = 10°C + 273.15 = 283.15 K

`S_(cold) = k * ln(V_(cold)) + C_v * ln(T_(cold))`

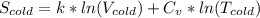
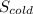`S_{cold` = 1.38 × 10⁻²³ J/K × ln(25 liters) + 4.184 J/g°C × ln(283.15 K)

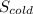`S_{cold` = 593.1 J/K

Calculate the total entropy of the mixture:

`V_(total) = V_(hot) + V_{cold`

= 50 liters + 25 liters

= 75 liters

`T_(final) = (m_(hot) * T_(hot) + m_(cold) * T_(cold)) / (m_(hot) + m_(cold))`

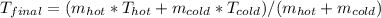
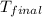`T_{final` = (50 kg × 55°C + 25 kg × 10°C) / (50 kg + 25 kg)

`T_{final` = 38.33°C

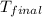`T_(final)_{K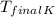` = 38.33°C + 273.15

= 311.48 K

`S_(final) = k * ln(V_(total)) + C_v * ln(T_(final)_(K))`

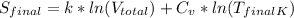
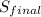`S_{final` = 1.38 × 10⁻²³ J/K × ln(75 liters) + 4.184 J/g°C × ln(311.48 K)

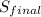`S_{final` = 789.2 J/K

Calculate the change in entropy:

`\Delta S = S_(final) - (S_(hot) + S_(cold))`

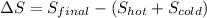
ΔS = 789.2 J/K - (658.7 J/K + 593.1 J/K)

ΔS ≈ 137.4 J/K

Therefore, you have created approximately 137.4 J/K of new entropy by mixing the hot and cold water.