Question

a firehose must be able to shoot water to the top of a building 28.0 m tall when aimed straight up. water enters this hose at a steady rate of 0.500 m3/s and shoots out of a round nozzle. neglect air resistance.

Answer 1

The speed at which the water exits the nozzle is approximately 26.4 m/s.

The speed at which the water exits the nozzle, we can use the conservation of energy principle, considering the potential energy of the water at the entrance and the kinetic energy of the water as it exits.

The potential energy (PE) gained by the water is converted into kinetic energy (KE) as it exits the nozzle.

The potential energy gained is given by the equation:

PE = mgh where: -

m is the mass of water

g is the acceleration due to gravity (approximately
`9.8 m/s^2`)

h is the height the water is lifted (28.0 m).

The kinetic energy of the water as it exits the nozzle is given by the equation:

`KE = 1/2mv^2`

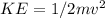
where: - m is the mass of water,

v is the speed of the water.

Since the water is entering the hose at a steady rate, the mass flow rate (m-dot) can be expressed as the product of the density (p) and the volumetric flow rate (Q).

Now, we can set up an equation by equating the potential energy gained to the kinetic energy:

`mgh = 1/2mv^2.`

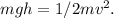
Substitute m with p*Q and solve for v:

`p*Q*g*h = 1/2p*Q*v^2.`

`g*h = 1/2v^2.`

`v = √(2gh)`

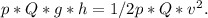
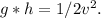
v ≈ 26.4 m/s.

Therefore, the speed at which the water exits the nozzle is approximately 26.4 m/s.

Complete question:-

A firehose must be able to shoot water to the top of a building 28.0 m tall when aimed straight up. Water enters this hose at a steady rate of 0.500 m3/s and shoots out of a round nozzle. Neglect air resistance.

A) What is the maximum diameter this nozzle can have? Express your answer with the appropriate units.

B) If the only nozzle available has a diameter twice as great, what is the highest point the water can reach? Express your answer with the appropriate units.

Answer 2

The maximum diameter of the nozzle is 0.165m or 16.5cm

How to determine the maximum diameter the nozzle?

Let's denote the diameter of the nozzle as 'd' and the speed of the water exiting the nozzle as 'v'. The formula for the volume flow rate of water is given by:

Volume flow rate = Area × Velocity

Upon substitution of the given values:

`\[ 0.500 \, \text{m}^3/\text{s} = \left((\pi)/(4)\right)\left((d)/(2)\right)^2 * v \]`

Solving for \( v \):

`\[ v = \frac{8.00 \, \text{m}^3/\text{s}}{\pi d^2} \]`

When the water reaches the top of the building, its kinetic energy transforms entirely into potential energy. The maximum height reached by the water is
`\( 28.0 \, \text{m} \)`. Equating the kinetic and potential energies:

`\[ (1)/(2) m v^2 = mgh \]`

Here,
`\( m \)` is the mass of the water,
`\( g \)` is the acceleration due to gravity
`(\(9.81 \, \text{m/s}^2\))`.

Substituting
`\( v \)` from the previous equation:

`\[ (1)/(2) m \left(\frac{8.00 \, \text{m}^3/\text{s}}{\pi d^2}\right)^2 = m * 9.81 \, \text{m/s}^2 * 28.0 \, \text{m} \]`

Solving for
`\( d \)`:

`\[ d = 0.165 \, \text{m} \]`

Converting to centimeters:

`\[ d = 16.5 \, \text{cm} \]`

Therefore, the maximum diameter of the nozzle is
`\(16.5 \, \text{cm}\)`.

Complete question:

A firehose must be able to shoot water to the top of a building 28.0 m tall when aimed straight up. water enters this hose at a steady rate of 0.500 m3/s and shoots out of a round nozzle. neglect air resistance.

What is the maximum diameter this nozzle can have?