
To determine the rate of simple interest at which an amount grows to
 of the principal in 2.5 years, we can use the formula for simple interest:
of the principal in 2.5 years, we can use the formula for simple interest:
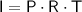
where:
 is the interest earned,
is the interest earned,
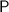 is the principal amount,
is the principal amount,
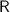 is the rate of interest, and
is the rate of interest, and
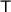 is the time period.
is the time period.
Given that the amount after 2.5 years is
 of the principal, we can set up the equation:
of the principal, we can set up the equation:
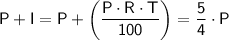
Simplifying the equation, we get:
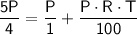
Now, let's solve for the rate of interest,
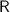 . We can rearrange the equation as follows:
. We can rearrange the equation as follows:

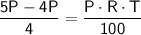
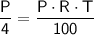
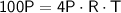
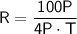
Simplifying further, we find:
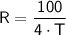
Substituting the given time period of 2.5 years, we get:

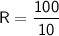
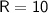
Therefore, the rate of simple interest required for the amount to grow to
 of the principal in 2.5 years is 10%.
of the principal in 2.5 years is 10%.

♥️
