Question

Suppose that the average stock has a volatility of 45%​, and that the correlation between pairs of stocks is 25%. Estimate the volatility of an equally weighted portfolio​ with:

a. 1 stock

b. 30 stocks

c. 1,000 stocks

Answer 1

The volatility of a portfolio with 1 stock is 45%. With 30 stocks, the portfolio's volatility is lower due to diversification benefits. With 1,000 stocks, the volatility is even lower, though diversification benefits diminish after a certain point.

Step-by-step explanation:

When estimating the volatility of a portfolio, it's important to consider two things: the average volatility of the individual stocks in the portfolio, which is 45%, and the average correlation between pairs of stocks, which is 25%. The volatility of the portfolio depends on these two factors, as well as the number of stocks in the portfolio.

Volatility Estimation:

• With 1 stock, the portfolio's volatility is simply the stock's volatility, so it would be 45%.
• For a portfolio with 30 stocks, we would use the formula for portfolio variance, which includes terms for the variance of the individual securities and their co-variances due to correlations. The volatility would be less than the individual stock volatility of 45% because diversification reduces risk.
• For a portfolio with 1,000 stocks, the diversification effect would be even more pronounced, resulting in a lower overall portfolio volatility compared to having just one stock or 30 stocks.

It's valuable to note that as the number of stocks in a portfolio increases, diversification benefits are gained which reduces the overall portfolio volatility up to a certain point. Beyond a certain number of stocks, additional diversification will not significantly reduce the additional risk.

Answer 2

The portfolio volatility is 25.6%

To estimate the volatility of an equally weighted portfolio, we can use the following formula:

Portfolio Volatility = σ * √(1 - ρ/N)

Where:

σ = Volatility of individual stocks

ρ = Correlation between pairs of stocks

N = Number of stocks in the portfolio

a. 1 stock

For a single stock, the portfolio volatility is simply equal to the volatility of the individual stock:

Portfolio Volatility =
`45/100 * \sqrt(1 - 0.25/1) = 43.3%`

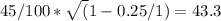
b. 30 stocks

With 30 stocks, the portfolio volatility decreases due to the diversification effect:

Portfolio Volatility =
`45/100 * \sqrt(1 - 0.25/30) ≈ 39.5%`

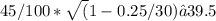
c. 1,000 stocks

With 1,000 stocks, the portfolio volatility is expected to approach the minimum achievable volatility, which is equal to the standard deviation of individual stock returns multiplied by the square root of the correlation between them:

Minimum Volatility =
`45/100 * √((0.25)) = 26.5%`

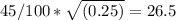
For an equally weighted portfolio of 1,000 stocks, the portfolio volatility is very close to the minimum achievable volatility:

Portfolio Volatility =
`45/100 * √((1 - 0.25/1000)) ≈ 26.6%`