Question

Solve (9th grade math)

Answer 1

1. Geometric Sequence Equation for Table A:

`\boxed{\tt a_n = a_1 * r^((n-1))}`

2. Arithmetic Sequence Equation for Table B:

`\boxed{\tt a_n = a_1 + (n-1) * d}`

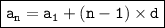
3.

• 20th term for Geometric Sequence:
  
  `\boxed{\tt a_(20) = a_1 * r^(19)}`

• 20th term for Geometric Sequence:
  
  `\boxed{\tt a_(20) = a_1 + 19* d}`

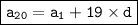
Explanation:

1. Geometric Sequence Equation for Table A:

The geometric sequence equation is given by the formula:

`\tt \[a_n = a_1 * r^((n-1))\]`

where:

• 
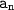  `\tt \(a_n\)` represents the nth term of the sequence.

• 
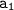  `\tt \(a_1\)` is the first term of the sequence.

• 
  `\tt \(r\)` is the common ratio.

For Table A, since we don't have the actual values, we can represent the equation as:

`\boxed{\tt a_n = a_1 * r^((n-1))}`

`\hrulefill`

2. Arithmetic Sequence Equation for Table B:

The arithmetic sequence equation is given by the formula:

`\tt a_n = a_1 + (n-1) * d`

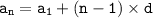
where:

• 
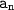  `\tt \(a_n\)` represents the nth term of the sequence.
• 
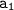  `\tt \(a_1\)` is the first term of the sequence.
• 
  `\tt \(d\)` is the common difference.

For Table B, since we don't have the actual values, we can represent the equation as:

`\boxed{\tt a_n = a_1 + (n-1) * d}`

`\hrulefill`

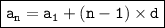
3. Finding Term 20 for both sequences:

In order to find the 20th term for both sequences, we need the actual values for
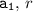`\tt \(a_1\), \(r\)` and d.

in the case of Table A

`\tt a_(20) = a_1 * r^((20-1))`

`\boxed{\tt a_(20) = a_1 * r^(19)}`

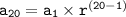
in the case of Table B.

`\tt a_(20) = a_1 + (20-1) * d`

`\boxed{\tt a_(20) = a_1 + 19* d}`

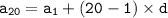
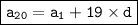
By using this formula, we can easily fill up the box.