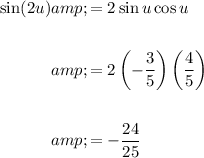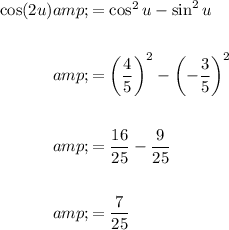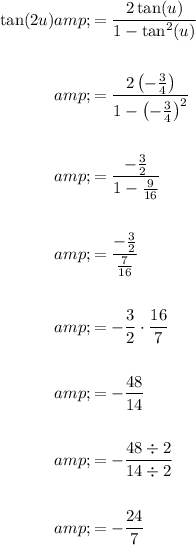Question

Use the given conditions to find the exact values of sin(2u), cos(2u), and tan(2u) using the double-angle formulas.

sin(u) = -3/5, 3π/2 < u < 2π
sin(2u) =
cos(2u) =
tan(2u)

Answer 1

`\sin(2u)=-(24)/(25)`

`\cos(2u)=(7)/(25)`

`\tan(2u)=-(24)/(7)`

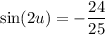
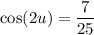
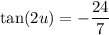
Explanation:

Given sin(u) = -3/5, use the trigonometric identity sin²θ + cos²θ = 1 to find cos(u):

`\begin{aligned}\sin^2(u)+\cos^2(u)&=1\\\\\left(-(3)/(5)\right)^2+\cos^2(u)&=1\\\\(9)/(25)+\cos^2(u)&=1\\\\\cos^2(u)&=1-(9)/(25)\\\\\cos^2(u)&=(16)/(25)\\\\\cos(u)&=(4)/(5)\end{aligned}`

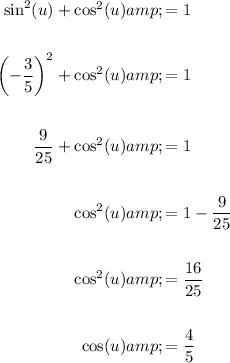
As u is in the interval 3π/2 < u < 2π, the angle is in quadrant IV of the unit circle. In quadrant IV, cos is positive and sin is negative. Therefore:

`\sin(u)=-(3)/(5) \qquad \cos(u)=(4)/(5)`

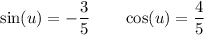
Calculate tan(u) by using the identity tanθ = sinθ/cosθ:

`\tan(u)=(-(3)/(5))/((4)/(5))=-(3)/(4)`

`\boxed{\begin{minipage}{5 cm}\underline{Double Angle Identities}\\\\$\sin (2\theta)=2\sin \theta \cos \theta $\\\\$\cos (2\theta)=\cos^2\theta-\sin^2\theta$\\\\$\tan (2\theta)=(2\tan\theta)/(1 -\tan^2\theta)$\\\end{minipage}}`

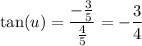
Use the double angle identities to find sin(2u), cos(2u) and tan(2u).

`\hrulefill`

`\begin{aligned}\sin (2u)&=2\sin u \cos u\\\\&=2\left(-(3)/(5)\right) \left((4)/(5)\right)\\\\&=-(24)/(25)\end{aligned}`

`\hrulefill`

`\begin{aligned}\cos (2u)&=\cos^2u - \sin^2u\\\\&=\left((4)/(5)\right)^2-\left(-(3)/(5)\right)^2\\\\&=(16)/(25)-(9)/(25)\\\\&=(7)/(25)\end{aligned}`

`\hrulefill`

`\begin{aligned}\tan (2u)&=(2\tan(u))/(1 -\tan^2(u))\\\\&=(2\left(-(3)/(4)\right))/(1 -\left(-(3)/(4)\right)^2)\\\\&=(-(3)/(2))/(1 -(9)/(16))\\\\&=(-(3)/(2))/((7)/(16))\\\\&=-(3)/(2) \cdot (16)/(7)\\\\&=-(48)/(14)\\\\&=-(48/2)/(14/2)\\\\&=-(24)/(7)\end{aligned}`