Answer:
For 1st:
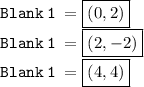
For 2nd: b. 6
For 3rd: b. 1
For 4th: c. reflection
Explanation:
For 1st Question:
The reflection of a point P (x, y) on the x-axis is a point P' (x, -y).
This means that the x-coordinate of the reflected point is the same as the original point, but the y-coordinate is the opposite sign.
P(x, y) on the x-axis is a point P'(x, -y).
R(0,-2)
 R'(0,2)
R'(0,2)
E(2,2 )
 E'(2,-2)
E'(2,-2)
F(4,-4)
 F'(4,4)
F'(4,4)
 For 2nd Question:
For 2nd Question:
A regular hexagon has 6 lines of symmetry. These lines of symmetry divide the hexagon into 6 congruent parts.
- The lines of symmetry of a regular hexagon are the lines that pass through the center of the hexagon and connect opposite vertices or connect the midpoints of opposite sides.
Therefore, answer is b. 6
For 3rd Question:
If a trapezoid is located entirely in quadrant II, then all of its points will have a positive x-coordinate and a negative y-coordinate. When the trapezoid is reflected across the x-axis, the x-coordinates of all of its points will stay the same, but the y-coordinates will become positive. Therefore, the new trapezoid will be located entirely in quadrant I.
Quadrant II
 Quadrant I
Quadrant I
(x, -y)
 (x, -y)
(x, -y)
As you can see, the point (x, y) is located in quadrant II, but its reflection (x, -y) is located in quadrant I.
Therefore, the new trapezoid will be located in quadrant 1.
So the answer is b. 1.

For 4th Question:
If all the coordinates of triangle ABC are from quadrant II to quadrant I, then the triangle must have been reflected across the x-axis.
This is because the x-coordinates of all the points in quadrant II are negative, but the x-coordinates of all the points in quadrant I are positive.
When a point is reflected across the x-axis, its x-coordinate stays the same, but its y-coordinate is negated.
Quadrant II
 Quadrant I
Quadrant I
(x, y)
 (x, -y)
(x, -y)
As you can see, the point (x, y) is located in quadrant II, but its reflection (x, -y) is located in quadrant I.
Therefore, the triangle must have been reflected across the x-axis.
So the answer is c. reflection.