Question

PART ONE:

A cylinder with moment of inertia 31.1 kg m2
rotates with angular velocity 6.95 rad/s on a
frictionless vertical axle. A second cylinder,
with moment of inertia 32.3 kg m2, initially
not rotating, drops onto the first cylinder and
remains in contact. Since the surfaces are
rough, the two eventually reach the same angular velocity.
Calculate the final angular velocity.
Answer in units of rad/s.

PART TWO:
Show that energy is lost in this situation by
calculating the ratio of the final to the initial
kinetic energy

Answer 1

Part one: final angular velocity: 3.409 rad/s

Part two: ratio of the final to the initial kinetic energy: 0.49

Step-by-step explanation:

PART ONE

The final angular velocity of the two cylinders is given by the following equation:

`\boxed{\tt \omega_(final )= (I_1 \omega_1)/(I_1 + I_2)}`

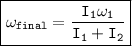
where:

`\tt \omega_(final)` is the final angular velocity (in rad/s)

• 
  `I_1` is the moment of inertia of the first cylinder (in kg m^2)
• 
  `\tt \omega_1` is the initial angular velocity of the first cylinder (in rad/s)
• 
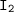  `\tt I_2` is the moment of inertia of the second cylinder (in kg m^2)

In this case, we have:

• 
  `\tt I_1 = 31.1 kg \:m^2`

• 
  `\tt \omega_1 = 6.95 rad/s`

• 
  `\tt I_2 = 32.3 kg\: m^2`

Substituting these values into the equation, we get:

`\tt \omega_(final) = (31.1 \cdot 6.95)/(31.1 + 32.3) = 3.409 \text{ rad/s}`

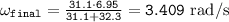
Therefore, the final angular velocity of the two cylinders is 3.409 rad/s.

PART TWO

in order to show that energy is lost in this situation, we can calculate the ratio of the final to the initial kinetic energy.

The kinetic energy of a rotating cylinder is given by the following equation:

`\boxed{\tt K = (1)/(2) I \omega^2}`

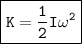
where:

• K is the kinetic energy (in J)

• I is the moment of inertia (in kg m^2)

• 
  `\omega` is the angular velocity (in rad/s)

The initial kinetic energy of the first cylinder is:

`\tt K_(initial) = (1)/(2) I_1 {\omega_1}^2 = (1)/(2) *31.1 * (6.95)^2 = 751.10 \text{ J}`

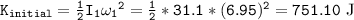
The final kinetic energy of the two cylinders is:

`\tt K_(final )= (1)/(2) (I_1 + I_2) {\omega_(final)}^2 = (1)/(2) * (31.1+32.3) * (3.409)^2 = 368.39 \text{ J}`

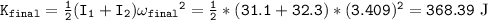
The ratio of the final to the initial kinetic energy is:

`\tt (K_(final))/(K_(initial)) = (368.39)/(751.10) = 0.49`

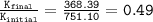
that means that 51% of the initial kinetic energy was lost in the collision.