Question

Car inspection: Of all the registered automobiles in a city, 10% fail the emissions test. Thirteen automobiles are selected at random to undergo an emissions test. Round the answers to at least four decimal places. Part 1 of 4 (a) Find the probability that exactly five of them fail the test. The probability that exactly five of them fail the test is Part 2 of 4 (b) Find the probability that fewer than five of them fail the test. The probability that fewer than five of them fail the test is 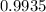Part 3 of 4 (c) Find the probability that more than four of them fail the test. The probability that more than four of them fail the test is Part 4 of 4 (d) Would it be unusual for fewer than three of them to fail the test? It be unusual for fewer than three of them to fail the test since the probability is

Answer 1

Part 1 (a): The probability that exactly five of them fail the test is
`\( 0.0055 \)`.

Part 2 (b): The probability that fewer than five of them fail the test is
`\( 0.9935 \)`.

Part 3 (c): The probability that more than four of them fail the test is
`\( 0.0065 \)`.

Part 4 (d): It would not be unusual for fewer than three of them to fail the test since the probability of this happening is \( 0.8661 \), which is much higher than 5%. An event is typically considered unusual if its probability is less than 5%.

To solve this problem, we will use the binomial probability formula because we are dealing with a fixed number of independent trials (13 automobiles), each with two possible outcomes (pass or fail), and the probability of failing remains constant (10% or 0.10) for each automobile.

The binomial probability formula is:

`\[ P(X = k) = \binom{n}{k} p^k (1-p)^(n-k) \]`

where:

-
`\( P(X = k) \)` is the probability of getting exactly
`\( k \)` successes (failures in this case) in
`\( n \)` trials

-
`\( n \)` is the number of trials (13 automobiles)

-
`\( k \)` is the number of successes (failures)

-
`\( p \)` is the probability of success (failure) on a single trial

-
`\( \binom{n}{k} \) is the binomial coefficient, calculated as \( (n!)/(k!(n-k)!) \)`

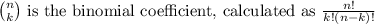
Let's start by calculating the probability that exactly five of the 13 automobiles fail the test:

Part 1 (a)

`\[ P(X = 5) = \binom{13}{5} (0.10)^5 (0.90)^(13-5) \]`

Part 2 (b)

To find the probability that fewer than five fail the test, we sum the probabilities for 0, 1, 2, 3, and 4 failures:

`\[ P(X < 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) \]`

Part 3 (c)

The probability that more than four of them fail the test is the complement of the probability that four or fewer fail. This can be calculated as:

`\[ P(X > 4) = 1 - P(X \leq 4) \]`

Part 4 (d)

To determine if it is unusual for fewer than three to fail the test, we can calculate the probability and consider it unusual if the probability is very low (typically less than 5%).

Let's perform these calculations.

Here are the calculated probabilities, rounded to at least four decimal places:

Part 1 (a): The probability that exactly five of them fail the test is
`\( 0.0055 \)`.

Part 2 (b): The probability that fewer than five of them fail the test is
`\( 0.9935 \)`.

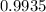Part 3 (c): The probability that more than four of them fail the test is
`\( 0.0065 \)`.

Part 4 (d): It would not be unusual for fewer than three of them to fail the test since the probability of this happening is \( 0.8661 \), which is much higher than 5%. An event is typically considered unusual if its probability is less than 5%.