Question

Statistics help! Check my maths please!

Look at images!!!!!!!!


James believes the honor roll students at his school have an unfair advantage in being assigned to the math class they request. He asked 500 students at his school the following questions: "Are you on the honor roll?" and "Did you get the math class you requested?" The results are shown in the table below:


Calculate P(received math class requested|Honor roll) and evaluate whether the two events appear independent.


A. p = 0.885; the events are independent because a student can be on the honor roll and receive the math class requested


B. p = 0.630; the events are not independent because the probability of any student receiving the class requested is 0.758


C. p = 0.885; the events are not independent because the probability of any student receiving the class requested is 0.758


D. p = 0.630; the events are independent because a student can be on the honor roll and receive the math class requested

Answer 1

Your work is correct

C. p = 0.885; the events are not independent because the probability of any student receiving the class requested is 0.758

Explanation:

Calc P(math | honor):

`P(math\;\cap\;honor)=(315)/(500) = 0.63\\\\P(honor) = (356)/(500) = 0.712`

`P(math | honor) =(P(math\;\cap\;honor))/(P(honor))\\\\= (0.63)/(0.712)\\ \\=0.885`

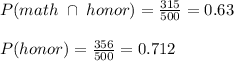
Check for Independence

Two events A and B are independent if P(A | B) = P(A)

The two events are independent if:

P(math | honor) = P(math)

P(math | honor) = 0.885

P(math) =
`(379)/(500) = 0.758`

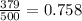
so, P(math | honor) ≠ P(math)

Therefore, the two events are not independent