Question

!50 POINTS! (4 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1. f) 15 inches

2. c) 9 yd, 6 yd, 5 yd

3. f) 5 inches

4. c) 3 yd, 5 ft, 8 ft

Explanation:

To solve the given problems, use the Triangle Inequality Theorem.

Triangle Inequality Theorem

The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

`\hrulefill`

Question 1

We have been told that two sides of the triangle are 9 inches and 6 inches.

Let "x" be the length of the third of the triangle.

Using the Triangle Inequality Theorem, we can write the following inequalities:

`9+6 > x \implies x < 15`

`9+x > 6\implies x > -3`

`6+x > 9\implies x > 3`

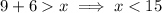
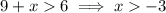
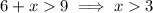
Combining the solutions, the range of possible lengths for the third side is 3 < x < 15.

Therefore, the length that cannot be the remaining side is 15 inches.

`\hrulefill`

Question 2

To be able to form a triangle with three given sides, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Given group of side lengths: 9 yd, 6 yd, 5 yd.

`9+6 > 5 \quad \checkmark`

`9+5 > 6 \quad \checkmark`

`5+6 > 9 \quad \checkmark`

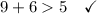
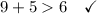
Therefore, a triangle can be formed with sides measuring 9 yd, 6 yd and 5 yd.

Given group of side lengths: 5 in, 8 in, 2 in.

`5+8 > 2 \quad \checkmark`

`2+8 > 5 \quad \checkmark`

`5+2 \\gtr 8`

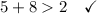
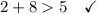
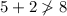
Therefore, a triangle cannot be formed with sides measuring 5 in, 8 in and 2 in.

Given group of side lengths: 1.2 m, 4.0 m, 1.8 m.

`1.2+4.0 > 1.8 \quad \checkmark`

`1.8+4.0 > 1.2 \quad \checkmark`

`1.2+1.8 \\gtr 4.0`

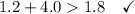
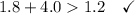
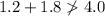
Therefore, a triangle cannot be formed with sides measuring 1.2 m, 4.0 m and 1.8 m.

Given group of side lengths: 1 ft, 5 ft, 6 ft.

`5+6 > 1 \quad \checkmark`

`6+1 > 5 \quad \checkmark`

`5+1 \\gtr 6`

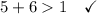
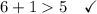
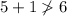
Therefore, a triangle cannot be formed with sides measuring 1 ft, 5 ft and 6 ft.

Therefore, only 9 yd, 6 yd and 5 yd could be the side lengths of a triangle.

`\hrulefill`

Question 3

We have been told that two sides of the triangle are 5 inches and 9 inches.

Let "x" be the length of the third of the triangle.

Using the Triangle Inequality Theorem, we can write the following inequalities:

`5+9 > x \implies x < 14`

`9+x > 5\implies x > -4`

`5+x > 9\implies x > 4`

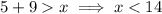
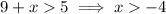
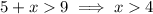
Combining the solutions, the range of possible lengths for the third side is 4 < x < 14.

Therefore, the length that could be the measure of the third side is 5 inches.

`\hrulefill`

Question 4

To determine which group of side lengths could be used to construct a triangle, we first need to ensure the side lengths are in the same units of measurement.

As 1 ft = 12 in, then 2 ft = 24 in.

Therefore, the group of side lengths is: 24 in, 11 in, 12 in.

`24+11 > 12 \quad \checkmark`

`24+12 > 11 \quad \checkmark`

`11+12\\gtr 24`

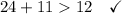
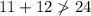
Therefore, a triangle cannot be formed with sides measuring 2 ft, 11 in and 12 in.

As 1 yd = 3 ft, then 3 yd = 9 ft.

Therefore, the group of side lengths is: 9 ft, 5 ft, 8 ft.

`9+5 > 8 \quad \checkmark`

`9+8 > 5 \quad \checkmark`

`5+8 > 9 \quad \checkmark`

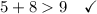
Therefore, a triangle can be formed with sides measuring 3 yd, 5 ft and 8 ft.

Given group of side lengths: 11 in, 16 in, 27 in.

`11+27 > 16 \quad \checkmark`

`16+27 > 11 \quad \checkmark`

`16+11\\gtr 27`

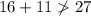
Therefore, a triangle cannot be formed with sides measuring 11 in, 16 in and 27 in.

As 1 yd = 3 ft, then 3 yd = 9 ft, and 5 yd = 15 ft.

Therefore, the group of side lengths is: 9 ft, 4 ft, 15 ft.

`9+15 > 4 \quad \checkmark`

`4+15 > 9 \quad \checkmark`

`4+9\\gtr 15`

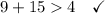
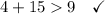
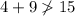
Therefore, a triangle cannot be formed with sides measuring 3 yd, 4 ft and 5 yd.

Therefore, the only group of sides that can form a triangle is 3 yd, 5 ft, 8 ft.