Question

A public health official responding to an outbreak of measles needs to estimate the vaccination rate in the community. The official will use a confidence interval of ' 95

′
% and a margin of error of ' 2%, but they do not have an estimate for the population proportion.

Answer 1

The public health official would need a sample size of approximately 2401 individuals from the community to estimate the vaccination rate with a 95% confidence level and a maximum margin of error of 2%, assuming they have no prior estimate of the population proportion.

How we arrived at the solution

In order to estimate the vaccination rate in the community with a confidence interval of 95% and a margin of error of 2%, the public health official can use the maximum margin of error formula without an estimate for the population proportion. The maximum margin of error occurs when the population proportion is assumed to be 0.5 (which gives the most conservative estimate in terms of variability).

The formula for the maximum margin of error is:

Maximum margin error = Critical value ×
`\sqrt{(p(1-p))/(n) }`

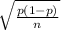
Where:

Critical value is is the z-score associated with the desired confidence level (95% in this case). For a 95% confidence interval, the z-score is approximately 1.96.

n = is the sample size.

p = is the estimated population proportion (assuming 0.5 for maximum variability).

Given that the margin of error is 2%, which is 0.02 in decimal form, and using Critical value = 1.96 for a 95% confidence level, we can rearrange the formula to solve for the required sample size (n):

0.02 = 1.96 ×
`\sqrt{(0.5(1-0.5))/(n) }`

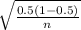
Squaring both sides to solve for n:

(0.02)² = (1.96)² ×
`(0.5(1-0.5))/(n)`

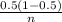
0.0004 = 3.8416 ×
`(0.25)/(n)`

n =
`(3.8416 * 0.25 )/(0.0004)`

n ≈ 2401