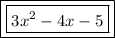Question

Divide( use long division):
6×^3+2x-17x^2+15 by 2x-3​

Answer 1

3x² - 4x - 5

Explanation:

Definitions:

• Dividend: The polynomial which has to be divided.
• Divisor: The expression by which the dividend is divided.
• Quotient: The result of the division.
• Remainder: The part left over.

Long Division Method of dividing polynomials:

• Divide the first term of the dividend by the first term of the divisor and put that in the answer.
• Multiply the divisor by that answer, put that below the dividend and subtract to create a new polynomial.
• Repeat until no more division is possible.
• Write the solution as the quotient plus the remainder divided by the divisor.

Given:

• Dividend: 6x³ + 2x - 17x² + 15
• Divisor: 2x - 3

Rearrange the dividend in descending order of the exponents:

6x³ - 17x² + 2x + 15

Now use the method of long division to divide (6x³ - 17x² + 2x + 15) by (2x - 3):

`\large \begin{array}{r}3x^2-4x-5\phantom{)}\\2x-3{\overline{\smash{\big)}\,6x^3-17x^2+2x+15\phantom{)}}}\\{-~\phantom{(}\underline{(6x^3-9x^2)\phantom{-b)))))))).)}}\\-8x^2+2x+15\phantom{)}\\-~\phantom{()}\underline{(-8x^2+12x)\phantom{)))..}}\\-10x+15\phantom{)}\\-~\phantom{()}\underline{(-10x+15)\phantom{}}\\0\phantom{)}\\\end{array}`

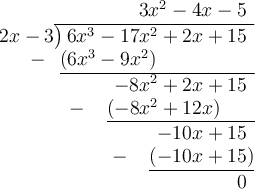
Therefore, the quotient is:

`\boxed{\boxed{3x^2-4x-5}}`