Answer:
The new angular velocity of the merry-go-round is 18.388 revolutions per minute.
Step-by-step explanation:
The merry-go-round can be represented by a solid disk, whereas the three children can be considered as particles. Since there is no external force acting on the system, we can apply the principle of angular momentum conservation:
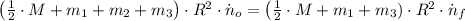 (1)
(1)
Where:
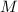 - Mass of the merry-go-round, in kilograms.
- Mass of the merry-go-round, in kilograms.
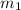 ,
,
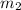 ,
,
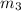 - Masses of the three children, in kilograms.
- Masses of the three children, in kilograms.
 - Radius of the merry-go-round/Distance of the children with respect to the center of the merry-go-round, in meters.
- Radius of the merry-go-round/Distance of the children with respect to the center of the merry-go-round, in meters.
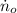 ,
,
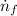 - Initial and final angular speed, in revolutions per minute.
- Initial and final angular speed, in revolutions per minute.
If we know that
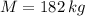 ,
,
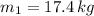 ,
,
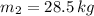 ,
,
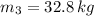 ,
,
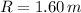 and
and
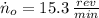 , then the final angular speed of the system is:
, then the final angular speed of the system is:
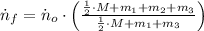
![\dot n_(f) = \left(15.3\,(rev)/(min) \right)\cdot \left[((1)/(2)\cdot (182\,kg) + 17.4\,kg +28.5\,kg + 32.8\,kg )/((1)/(2)\cdot (182\,kg) + 17.4\,kg + 32.8\,kg ) \right]](https://img.qammunity.org/qa-images/2022/formulas/physics/college/q2ysntpme1zfltajfxtt0c.png)
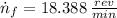
The new angular velocity of the merry-go-round is 18.388 revolutions per minute.