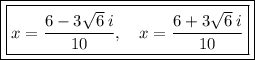Question

What are the roots of x in -10x^2+12x-9=0

Answer 1

Roots of x.

`\boxed{\boxed{\tt x = (6 - 3√(-6))/(10)} \: \tt \:and \: \boxed{\tt x = (6 + 3√(-6))/(10)}}`

Explanation:

The roots of any equation can be found using the quadratic equation formula:

`\boxed{\boxed{\tt x = (-b \pm √(b^2 - 4ac))/(2a)}}`

For the question:

`\tt -10x^2+12x-9=0` comparing this equation with
`\tt ax^2+bx+c=0`

we get,

a = -10, b = 12, and c = -9.

Substituting these values into the formula, we get:

`\tt x = (-12 \pm √(12^2 - 4 * -10 * -9))/(2 * -10)`

`\tt x = (-12 \pm √(-216))/(-20)`

`\tt x = (-12 \pm 6√(-6))/(-20)`

The roots of the equation are:

Taking Positive:

`\tt x = (-12 + 6√(-6))/(-20)`

`\tt x = (-2*(6 - 3√(-6)))/(-20)`

`\tt x = (6 - 3√(-6))/(10)`

Taking Negative:

`\tt x = (-12 - 6√(-6))/(-20)`

`\tt x = (-2*(6 + 3√(-6)))/(-20)`

`\tt x = (6 + 3√(-6))/(10)`

Therefore, Roots are:
`\boxed{\tt x = (6 - 3√(-6))/(10)} \: \tt \:and \: \boxed{\tt x = (6 + 3√(-6))/(10)}`

Answer 2

`x=(6 - 3√(6)\:i)/(10),\quad x=(6 +3√(6)\:i)/(10)`

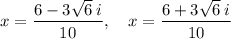
Explanation:

To find the roots of a quadratic equation in the form ax² + bx + c = 0, use the quadratic formula.

`\boxed{\begin{minipage}{5cm}\underline{Quadratic Formula}\\\\$x=(-b \pm √(b^2-4ac))/(2a)$\\\\when $ax^2+bx+c=0$ \\\end{minipage}}`

Compare the coefficients of the given quadratic equation -10x² + 12x - 9 = 0 to ax² + bx + c = 0:

• a = -10
• b = 12
• c = -9

Substitute the values of a, b and c into the quadratic formula:

`x=(-12 \pm √((12)^2-4(-10)(-9)))/(2(-10))`

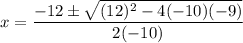
Simplify:

`x=(-12 \pm √(144-360))/(-20)`

`x=(12 \pm √(-216))/(20)`

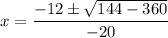
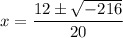
Rewrite -216 as 6² · 6 · (-1):

`x=(12 \pm √(6^2 \cdot 6 \cdot (-1)))/(20)`

`\textsf{Apply the radical rule:} \quad √(ab)=√(a)√(b)`

`x=(12 \pm √(6^2) √(6) √(-1))/(20)`

`\textsf{Apply the radical rule:} \quad √(a^2)=a, \quad a \geq 0`

`x=(12 \pm 6√(6) √(-1))/(20)`

`\textsf{Apply\;the\;imaginary\;number\;rule:}\quad √(-1)=i`

`x=(12 \pm 6√(6)\:i)/(20)`

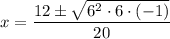
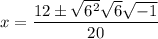
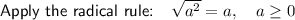
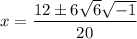
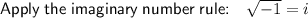
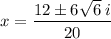
Divide by 2:

`x=(6 \pm 3√(6)\:i)/(10)`

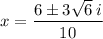
Therefore, the roots of the given quadratic equation are:

`\boxed{\boxed{x=(6 - 3√(6)\:i)/(10),\quad x=(6 +3√(6)\:i)/(10)}}`