Question

The weight of apples harvested from a certain orchard are normally distributed with a mean of 81 grams and a

standard deviation of 6.2 grams. What weight (to the nearest tenth) will separate the bottom 15% of apples from the
rest?
Your answer should be a decimal value rounded to the nearest tenth.
The weight that separates the bottom 15% from the rest is
grams.

Answer 1

Answer:2.07 is the answer as of e.2020

Step-by-step explanation:Mean = 270 Standard deviation = 10 x = 255 Formula for z-score, z = (x - mean)/SD z = (255 - 270) / 10 => z = -15 / 10 => z = -1.5 So by referring to z-table, -1.5 correlates to 0.0668 that implies to 0.07 So 7% of the boxes of Apples weight less than 255oz. The percentage of boxes is in the range of 255 oz and 270 oz, Now calculating the requiring percentage 50% - 7% = 43%

Answer 2

74.6 g

Explanation:

The weight of apples harvested from a certain orchard are normally distributed with a mean of 81 grams and a standard deviation of 6.2 grams.

Therefore, as the weight of apples are normally distributed:

`\boxed{X \sim\text{N} \left(81,6.2^2\right)}`

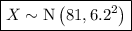
where X is the weight of the apples in grams.

To find the weight that will separate the bottom 15% of apples from the rest, we need to find the value of a for which P(X < a) = 15%.

Converting to the Z distribution:

`\boxed{\textsf{If }\: X \sim\textsf{N}(\mu,\sigma^2)\:\textsf{ then }\: (X-\mu)/(\sigma)=Z, \quad \textsf{where }\: Z \sim \textsf{N}(0,1)}`

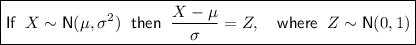
Transform X to Z:

`\text{P}(X < a) = \text{P}\left(Z < (a-81)/(6.2)\right)=0.15`

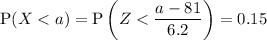
According to the z-tables, when p = 0.15, z = -1.0364. Therefore:

`\implies (a-81)/(6.2)\right)= -1.0364`

`\implies a-81= -6.42568`

`\implies a=74.57432`

`\implies a=74.6`

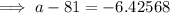
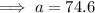
Therefore, the weight (to the nearest tenth) that will separate the bottom 15% of apples from the rest is 74.6 g.