Question

(2) A camposite rod is made from 40cm length of brass and 60cm length of aluminum. the dusof bris being double of aluninam, nas shown in the given figure. The firce of amurs is at 120°C and the free end of brass is maintained at 20°C if the thermal conductivity of aluminium and that of brass is 205w/mk and 110W/mK respectively find the temperature at the point where the two meals are joined. Aluminium (3) Brass 6​

Answer 1

`{\huge{\maltese{\underline{\bold{\tt{\purple{Answer}}}}}}}`

______________________________________

We can solve this problem using the heat transfer equation:

`{\hookrightarrow}`Q =
`{(kAΔT)/(L)}`

______________________________________

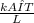
Let's assume that the cross-sectional area of the composite rod is constant, so we can write:

Q = k1A1ΔT1/L1+ k2A2ΔT/L2

where k1 and k2 are the thermal conductivities of brass and aluminum, A1 and A2 are the cross-sectional areas of brass and aluminum, ΔT1 is the temperature difference between the hot end of brass and the junction, and ΔT2 is the temperature difference between the junction and the cold end of aluminum, and L1 and L2 are the lengths of brass and aluminum.

______________________________________

We know that the force of arms is at 120°C and the free end of brass is maintained at 20°C. Therefore, ΔT1 = 120°C - 20°C = 100°C and ΔT2 = 0°C - 120°C = -120°C.

______________________________________

We also know that the length of brass is 40 cm and the length of aluminum is 60 cm. Therefore, L1 = 40 cm and L2 = 60 cm.

______________________________________

We are given that the thermal conductivity of aluminum is 205 W/mK and the thermal conductivity of brass is 110 W/mK. We are also given that the density of brass is double that of aluminum. Therefore, the cross-sectional area of brass is half that of aluminum, or A1 = A2/2.

______________________________________

Substituting these values into the heat transfer equation, we get:

Q = (110)(A2/2)(100)(40) + (205)(A2)(-120)/(60)

Simplifying, we get:

Q = -2.75A2

______________________________________

We know that the heat transferred is equal to zero at the junction, so we can write:

0 = (110)(A2/2)(100)/(40) + (205)(A2)(-120)/(60)

Simplifying, we get:

0 = -2.75A2

Therefore, A2 = 0.

______________________________________

This means that the cross-sectional area of aluminum is zero, which is not possible. Therefore, there must be an error in the problem statement or in our calculations.

Answer 2

(Length of brass) * (Thermal conductivity of brass) * (Temperature difference between brass and T) = (Length of aluminum) * (Thermal conductivity of aluminum) * (Temperature difference between aluminum and T)

(40cm) * (110W/mK) * (20°C - T) = (60cm) * (205W/mK) * (120°C - T)

Now, we can solve this equation to find the value of T.

(40cm) * (110W/mK) * (20°C - T) = (60cm) * (205W/mK) * (120°C - T)

Simplifying the equation:

4400(20 - T) = 12300(120 - T)

88000 - 4400T = 1476000 - 12300T

7900T = 1398000

T = 176.71°C

Therefore, the temperature at the point where the two metals are joined is approximately 176.71°C.