Question

Need some little help on this

Answer 1

NL= 7.81cm.

∡LNP= 39.8°

Area of shape =60 cm².

Explanation:

Given:

• LM=9 cm
• NO=15 cm
• MO=5cm

To find:

• NL
• ∡LNP
• Area of shape

Solution:

First find NP:

NP=NO-LM

Here, LM=PO opposite side of the rectangle is equal.

NP=15 cm - 9 cm=6 cm

Now

LP=MO=5 cm opposite side of the rectangle is equal.

By Using Pythagoras law, we can find NL

Since ΔLPN is right angled triangle.

NL is a hypotenuse(h):

Base(b) is LP and Perpendicular(p)is NP.

Using Pythagoras law:

`\boxed{\tt h^2=p^2+b^2}`

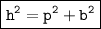
substituting value:

`\tt h^2=6^2+5^2`

`\tt h^2=61`

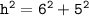
Doing square root on both side:

`\tt √(h^2)=√(61)`

`\tt h=7.81 cm`

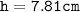
Therefore, NL is 7.81cm.

`\hrulefill`

To find ∡LNP, we can use sin law:

`\tt Sin \: N= (Opposite \:side\: of \:N )/(Hypotenuse)`

`\tt Sin\: N=(LP)/(LN)`

`\tt Sin\: N=(5)/(7.81)`

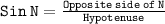
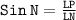
We can find ∡LNP, since ∡LNP is inverse of SIn N.

∡LNP=
`\tt sin^(-1)((5)/(7.81))=39.8^0`

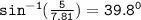
Therefore, ∡LNP=39.8°

`\hrulefill`

Area of the shape : Area of rectangle MOPL+ Area of triangle LPN

`\tt =length*breadth+(1)/(2)Base*Height`

`\tt =LM*MO+(1)/(2)LP*NP`

`\tt =9*5+(1)/(2)*5*6`

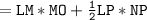
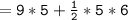
=60 cm²

Therefore, Area of Shape is 60 cm².