Question

If P increases by a factor of 5 and T decreases by a factor of 3, what will be the change in V?

A. V increases by a factor 3
B. V increases by a factor of 15
C. V decreases by 3/5
D. V increases by a factor 5
E. V decreases by a factor of 15

Answer 1

`\dag \: \: \: \huge{ \boxed{ \sf{ \pink{A\green{N \blue{S\color{yellow}W\red{E\orange{R}}}}}}}}`

To determine the change in volume (V) given the changes in pressure (P) and temperature (T), we need to consider the relationship described by the ideal gas law:

`\displaystyle PV = nRT`

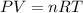
Where:

• - P is the pressure
• - V is the volume
• - n is the number of moles of gas
• - R is the ideal gas constant
• - T is the temperature

To analyze the effect of changing P and T on V, we'll assume that the number of moles (n) and the ideal gas constant (R) remain constant.

If P increases by a factor of 5, we can express the new pressure as:

`\displaystyle P_{\text{new}} = 5P`

If T decreases by a factor of 3, we can express the new temperature as:

`\displaystyle T_{\text{new}} = (1)/(3)T`

Now, let's consider the relationship between the initial and final volumes (V and V_new):

`\displaystyle PV = nRT`

`\displaystyle V = (nRT)/(P)`

`\displaystyle P_{\text{new}}V_{\text{new}} = nRT_{\text{new}}`

`\displaystyle V_{\text{new}} = \frac{nRT_{\text{new}}}{P_{\text{new}}}`

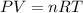
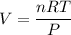
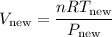
Substituting the expressions for P_new and T_new, we have:

`\displaystyle V_{\text{new}} = (nR\left((1)/(3)T\right))/(5P)`

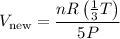
Simplifying the expression:

`\displaystyle V_{\text{new}} = (1)/(15)\left((nRT)/(P)\right)`

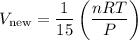
Comparing this with the initial volume (V), we can see that:

`\displaystyle V_{\text{new}} = (1)/(15)V`

Therefore, the change in volume (V) is such that it decreases by a factor of 15.

The correct option is E. V decreases by a factor of 15.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`