Question

A cylinder has a 12-inch diameter and is 15 inches tall. It is filled to the top with water. A 6-inch-diameter ball is placed within the cylinder, and then the cylinder is filled with water. How much water is in the cylinder? Give vour answer in terms of pi.

Answer 1

The radius of the cylinder is 6 inches, and its height is 15 inches. The volume of the cylinder is given by:

`\begin{aligned}\rm Volume_((Cylinder))& = \pi r^2 h \\& = \pi (6)^2 (15) \\& = 540\pi\end{aligned}`

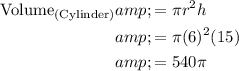
The radius of the ball is 3 inches. We can find the volume of the ball using the formula:

`\begin{aligned}\rm Volume_((Ball))& = (4)/(3) \pi r^3 \\& = (4)/(3) \pi (3)^3 \\ &= 36\pi\end{aligned}`

When the ball is placed inside the cylinder, it displaces some of the water. The volume of water displaced is equal to the volume of the ball. Thus, the volume of water that remains in the cylinder after the ball is placed inside is:

`\begin{aligned}\rm Volume_((Cylinder)) - Volume_((Ball))& = 540\pi - 36\pi\\& = 504\pi\end{aligned}`

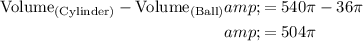
`\therefore` There are
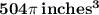`\bold{504\pi \: inches^3}` of water in the cylinder.

`\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}`