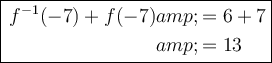Question

PLease solve it as fast has you can

Answer 1

The first time you have a problem is if you’re going through something and you’re trying something new you need a break and then you’re not doing anything to it so I think you’re going through a really hard situation right and then you’re just going to have a bad day so you don’t get it

Answer 2

`f^(-1)\left(f(576)\right)=\boxed{576}`

`f^(-1)(-7)+f(-7)=\boxed{13}`

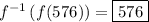
Explanation:

The inverse of an invertible function with the domain of all real numbers is obtained by reflecting the original function across the line y = x, which swaps the input and output values of the function. Therefore, (x, y) → (y, x).

Given table:

`\begin{array}{lrrrrrr}\vphantom{\frac12}x&-7&11&-13&6&5&-9\\\cline{1-7}\vphantom{\frac12}f(x)&7&12&8&-7&13&5\end{array}`

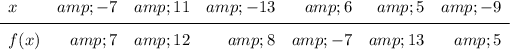
Inverse function:

`\begin{array}{lrrrrrr}\vphantom{\frac12}x&7&12&8&-7&13&5\\\cline{1-7}\vphantom{\frac12}f^(-1)(x)&-7&11&-13&6&5&-9\end{array}`

If we have a function f(x), the inverse function is denoted as f⁻¹(x), and it has the property that f⁻¹(f(x)) = x for all valid inputs x in the domain of f(x).

Therefore:

`\large\boxed{f^(-1)\left(f(576)\right)=576}`

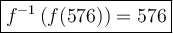
The value of f(-7) is the value of f(x) when x = -7. Therefore, reading from the original table, f(-7) = 7.

The value of f⁻¹(-7) is the value of f⁻¹(x) when x = -7. Therefore, reading from the inverse function table, f⁻¹(-7) = 6.

Therefore:

`\large\boxed{\begin{aligned}f^(-1)(-7)+f(-7)&=6+7\\&=13\end{aligned}}`