Question

Solve the following system of equations and show all work. y = −x2 + 4 y = 2x + 1 (10 points)

Answer 1

(1, 3) and (-3, -5)

Explanation:

Given the system of equations:

`\displaystyle{\begin{cases} y = -x^2+4 \\ y = 2x+1 \end{cases}}`

Since both are y-isolated equations, set the equation up equal each other:

`\displaystyle{2x+1=-x^2+4}`

Arrange the equation in quadratic:

`\displaystyle{x^2+2x+1-4=0}\\\\\displaystyle{x^2+2x+1=4}\\\\\displaystyle{\left(x+1\right)^2=4}`

Square root both sides and solve the rest:

`\displaystyle{√(\left(x+1\right)^2) = √(4)}\\\\\displaystyle{x+1=\pm √(4)}\\\\\displaystyle{x+1=\pm 2}\\\\\displaystyle{x=\pm 2-1}\\\\\displaystyle{x=1,-3}`

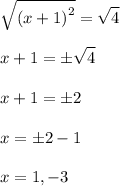
Next, substitute two x-values in either of those two equations. I'll substitute them in the second equation.

When x = 1,

`\displaystyle{y=2+1}\\\\\displaystyle{y=3}`

When x = -3,

`\displaystyle{y=2\left(-3\right)+1}\\\\\displaystyle{y=-6+1}\\\\\displaystyle{y=-5}`

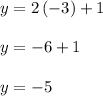
Therefore, the solutions are (1, 3) and (-3, -5).