Question

Complete the square to make a perfect square trinomial. Then, write the result as a binomial squared.

n2−6n

Answer 1

`\sf{\blue{«} \: \pink{ \large{ \underline{A\orange{N} \red{S} \green{W} \purple{E} \pink{{R}}}}}}`

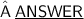
Given expression:
`\displaystyle\sf n^(2) -6n`

1. Take half of the coefficient of the linear term:

Half of
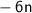`\displaystyle\sf -6n` is
`\displaystyle\sf -(6)/(2) = -3`.

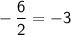2. Square the result obtained in step 1:

Squaring
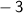`\displaystyle\sf -3` gives
`\displaystyle\sf (-3)^(2) = 9`.

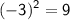3. Add the value obtained in step 2 to the original expression:

`\displaystyle\sf n^(2) -6n +9`

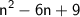
The result can be written as a binomial squared:

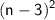
`\displaystyle\sf ( n-3)^(2)`

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`