Question

Ln(x³−2x²−x+2)−ln(x+1)−ln(x−2)=ln(2) solve

Answer 1

x = 3

Explanation:

Given the equation:

`\displaystyle{\ln \left(x^3-2x^2-x+2\right) - \ln \left(x+1\right) - \ln \left(x-2\right) = \ln 2}`

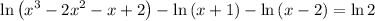
From x³ - 2x² - x + 2, it can be factored as:

`\displaystyle{ = x^2\left(x-2\right)-\left(x-2\right)}\\\\\displaystyle{=\left(x-2\right)\left(x^2-1\right)}\\\\\displaystyle{=\left(x-2\right)\left(x-1\right)\left(x+1\right)}`

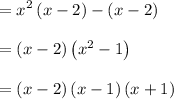
Thus, we will have:

`\displaystyle{\ln \left[ \left(x-2\right)\left(x-1\right)\left(x+1\right) \right]-\ln \left(x+1\right)-\ln \left(x-2\right)=\ln 2}`

We can apply the logarithm property where:

`\displaystyle{\ln \text{MNO} = \ln \text{M} + \ln \text{N} + \ln \text{O}}`

Hence,

`\displaystyle{\ln\left(x-2\right) + \ln \left(x-1\right) + \ln \left(x+1\right)-\ln \left(x+1\right)-\ln \left(x-2\right) = \ln 2}\\\\\displaystyle{\ln \left(x-1\right)=\ln 2}`

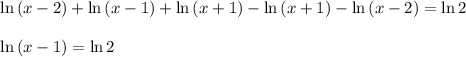
Since both sides have same logarithm, we can cancel the logarithm:

`\displaystyle{x-1=2}\\\\\displaystyle{x=3}`

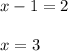
Since 3 > 1, x = 3 is the valid solution.