Question

A kangaroo can jump over an object 2.42 m high. calculate its vertical speed in m/s when it leaves the ground. (3 sig figs)

Answer 1

Approximately
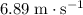`6.89\; {\rm m\cdot s^(-1)}` (assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`.)

Step-by-step explanation:

If air resistance on the kangaroo is negligible, the kangaroo would accelerate downward at a constant
`a = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}` while it is in the air.

Assume that the kangaroo reached a maximum height of exactly
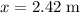`x = 2.42\; {\rm m}`. When the kangaroo is at the maximum height, vertical velocity of the kangaroo would be
`v = 0\; {\rm m\cdot s^(-1)}` (otherwise, the kangaroo would go up even further.)

The question is asking for the initial vertical velocity
`u` of this kangaroo. The following SUVAT equation relates this initial velocity to the current velocity
`v`, acceleration
`a`, and displacement
`x` of this kangaroo:

`v^(2) - u^(2) = 2\, a\, x`.

Rearrange this equation to find the initial vertical velocity
`u`:

`\begin{aligned}u &= \sqrt{v^(2) - 2\, a\, x} \\ &= √(0 - 2\, (-9.81)\, (2.42))\; {\rm m\cdot s^(-1)} \\ &\approx 6.89\; {\rm m\cdot s^(-1)}\end{aligned}`.

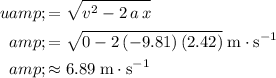In other words, the vertical speed of this kangaroo should be approximately
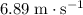`6.89\; {\rm m\cdot s^(-1)}` when leaving the ground.