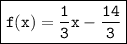Question

Write the linear function graphed below in slope intercept form using function notation

Answer 1

`\boxed{\tt f(x) = (1)/(3)x -(14)/(3)}`

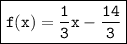
Explanation:

In order to find the linear function in slope-intercept form, we need to determine the slope (m) and the y-intercept (b) using the given points.

(2, -4) and (5, -3).

Let's find the slope (m):

`\boxed{\tt m = (change \:in \:y)/(change\: in\: x)}\\\tt m = (-3 - (-4))/(5 - 2)\\\tt m=(1)/(3)`

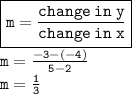
Now that we have the slope (m), we can use it along with one of the given points (2, -4) to find the y-intercept (b) using the slope-intercept form y=mx+b.

Using the point (2, -4):

Substituting value (x,y) in equation y=mx+b.

`\tt -4 =(1)/(3)*2 + b`

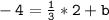
Simplifying:

`\tt -4 =(2)/(3)+ b`

Subtract
`(2)/(3)` from both sides:

`\tt -4 - (2)/(3) = b+ (2)/(3) - (2)/(3)`

`\tt b=(-4*3-2)/(3)`

`\tt b=(-14)/(3)`

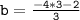
Now we have the slope and the y-intercept .

We can express the linear function in slope-intercept form as:

`\tt \bold{ f(x) = mx + b}\\\tt \bold{f(x) = (1)/(3)x +(-14)/(3)}`

`\boxed{\tt f(x) = (1)/(3)x -(14)/(3)}`

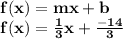
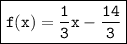
Therefore, the linear function graphed below in slope-intercept form using function notation, passing through (2, -4) and (5, -3) is :

`\boxed{\tt f(x) = (1)/(3)x -(14)/(3)}`