Question

what is the probability of obtaining a sample mean greater than m 5 60 for a random sample of n 5 16 scores selected from a normal population with a mean of m 5 65 and a standard deviation of s 5 20?what is the probability of obtaining a sample mean greater than m 5 60 for a random sample of n 5 16 scores selected from a normal population with a mean of m 5 65 and a standard deviation of s 5 20?

Answer 1

The probability of obtaining a sample mean greater than
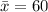`\(\bar{x} = 60\)`for a random sample of n = 16 from a normal population with
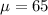`\(\mu = 65\)`and
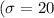`(\sigma = 20\)`) is approximately 0.0228 or 2.28%.

Explanation:

In this case, we are dealing with the distribution of sample means, which follows a normal distribution with a mean equal to the population mean
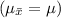`(\(\mu_{\bar{x}} = \mu\))` and a standard deviation equal to the population standard deviation divided by the square root of the sample size
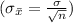`(\(\sigma_{\bar{x}} = (\sigma)/(√(n))\))`. For this problem,
`\(\mu_{\bar{x}} = 65\) and \(\sigma_{\bar{x}} = (20)/(√(16)) = 5\).`

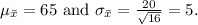
To find the probability of obtaining a sample mean greater than 60, we need to standardize the value using the z-score formula:
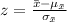`\(z = \frac{\bar{x} - \mu_{\bar{x}}}{\sigma_{\bar{x}}}\)`. Plugging in the values,
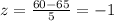`\(z = (60 - 65)/(5) = -1\)`. We then consult a standard normal distribution table or calculator to find the probability associated with \(z = -1\), which is approximately 0.0228 or 2.28%.

In conclusion, the probability of obtaining a sample mean greater than 60 is 2.28%. This result suggests that obtaining a sample mean as low as 60 is relatively unlikely given the characteristics of the population, reinforcing the influence of sample size on the distribution of sample means.

Answer 2

To calculate the probability of obtaining a sample mean greater than a given value, we can use the central limit theorem and the z-score formula. In this case, the probability of obtaining a sample mean greater than 60 for a random sample of size 16 from a normal population with a mean of 65 and a standard deviation of 20 is approximately 0.8413, or 84.13%.

Step-by-step explanation:

To calculate the probability of obtaining a sample mean greater than a given value, we can use the central limit theorem and the z-score formula.

1. First, we need to calculate the standard error of the mean, which is the standard deviation of the population divided by the square root of the sample size. In this case, the standard deviation is 20, and the sample size is 16, so the standard error of the mean is 20 / sqrt(16) = 5.
2. Next, we calculate the z-score using the formula: z = (x - μ) / standard error, where x is the mean we are interested in (60), μ is the population mean (65), and the standard error is 5. Substituting the values, we get z = (60 - 65) / 5 = -1.
3. Finally, we use a standard normal distribution table or calculator to find the probability of obtaining a z-score greater than -1. In this case, the probability is approximately 0.8413, or 84.13%.