Final Answer:
The simplified expression
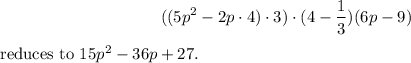
Step-by-step explanation:
To simplify the given expression, we'll follow the order of operations (PEMDAS/BODMAS - Parentheses/Brackets, Exponents/Orders, Multiplication and Division, and Addition and Subtraction).
1. Start by solving the expression inside parentheses:
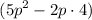 is equivalent to
is equivalent to
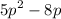 . The expression becomes
. The expression becomes
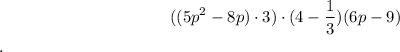
2. Next, simplify the remaining parts of the expression:
-
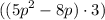 simplifies to
simplifies to

-
 simplifies to
simplifies to
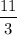 .
.
- Multiply
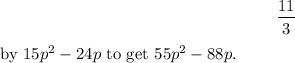
- Finally, multiply

3. The final step is to simplify
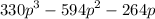 by factoring out the common factor of $66p$, resulting in
by factoring out the common factor of $66p$, resulting in

The simplified form is
 which can be expressed in the required form $ap - b$ as $15p - 36$.
which can be expressed in the required form $ap - b$ as $15p - 36$.