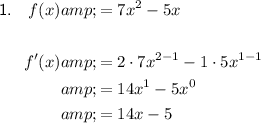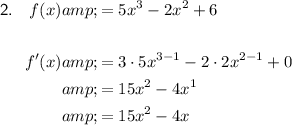Question

Can someone help me here please!thank you so much​ (with complete solution)​

Answer 1

1. f'(x) = 6x^2 + 10x - 3

2. f''(x) = 12x + 10

3. f'''(x) = 12

Answer 2

`\textsf{1.} \quad f'(x)=14x-5`

`\textsf{2.} \quad f'(x)=15x^2-4x`

`\textsf{3.} \quad f'(x)=12x`

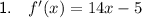
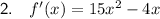
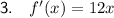
Explanation:

To find the derivatives of the given functions, we can use the power rule and the constant rule.

The power rule for differentiation states that when we differentiate a function that is a power of x, we multiply the function by its exponent, and then decrease the exponent by one:

`\boxed{\begin{minipage}{5.2 cm}\underline{Power Rule for Differentiation}\\\\$\frac{\text{d}}{\text{d}x}x^n=nx^(n-1)$\\\end{minipage}}`

The constant rule for differentiation states that the derivative of a constant is always zero:

`\boxed{\begin{minipage}{5.2cm}\underline{Constant Rule for Differentiation}\\\\$\frac{\text{d}}{\text{d}x}[c]=0$\\\end{minipage}}`

Therefore, we can apply these two rules to the given functions to find their derivatives.

`\hrulefill`

`\begin{aligned}\textsf{1.} \quad f(x)&=7x^2-5x\\\\f'(x)&=2\cdot 7x^(2-1)-1\cdot5x^(1-1)\\&=14x^1-5x^0\\&=14x-5\end{aligned}`

`\hrulefill`

`\begin{aligned}\textsf{2.} \quad f(x)&=5x^3-2x^2+6\\\\f'(x)&=3\cdot 5x^(3-1)-2\cdot2x^(2-1)+0\\&=15x^2-4x^1\\&=15x^2-4x\end{aligned}`

`\hrulefill`

`\begin{aligned}\textsf{3.} \quad f(x)&=6x^2+5\\\\f'(x)&=2\cdot 6x^(2-1)+0\\&=12x^1\\&=12x\end{aligned}`